When long-time pump users enter the compressor world, they must leave behind familiar flow terms, like GPM, GPH, BPH, etc. and embrace new terms, like SCFM, ICFM, CFM and ACFM, which define the flow of gases and vapors under pressure. By their compressible nature, gases require a different set of terms to define their flow. Here I will attempt to demystify this alphabet soup by explaining what these terms mean and how they are commonly used by practicing compressor professionals.
Ideal Gas Law
Before we can discuss flow definitions, we will cover some basic theory.
An ideal gas is one in which all collisions between atoms or molecules are perfectly elastic and in which there are no intermolecular attractive forces. Visualize it as a collection of perfectly hard spheres that collide, but otherwise do not interact with each other. In such a gas, all the internal energy is in the form of kinetic energy and any change in internal energy is accompanied by a change in temperature.
An ideal gas can be characterized by three state variables: absolute pressure (P), volume (V) and absolute temperature (T). The relationship between them may be deduced from kinetic theory and is called the ideal gas law:
PV=nRT
Where:
n = Number of moles
R = Universal gas constant = 8.3145 J/mol K
N = Number of molecules
k = Boltzmann constant = 1.38066 x 10-23 J/K = 8.617385 x 10-5 eV/K
k = R/NA
NA = Avogadro's number = 6.0221 x 1023 /mol
If the moles or weight in a given gas flowstream remains constant, we can write:
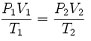 (Equation 1)
(Equation 1)
, where V can be in volume of volumetric flow for any two points in the flowstream.
Starting with Equation 1, we can determine gas volumes at different conditions, such as standard conditions and actual process conditions. Flow at standard conditions (SFCM) is defined as flow in cubic feet per minute of gas or air flow at standard conditions, which are typically set at 14.696 psia, 60 deg F (520deg R) and 0 percent relative humidity (RH). Actual cubic feet per minute (ACFM) stands for the cubic feet per minute of gas or air flow at the actual conditions inside the piping. A special distinction is given to flow at the conditions at the compressor inlet flange or nozzle. This flow is called inlet cubic feet per minute (ICFM), which is often used by compressor designers to determine actual gas or air velocities inside their machines.
If the process was moving a gas at exactly the "standard" condition, then ACFM would equal SCFM. Unfortunately, this is usually not the case as process temperatures and pressure change from one point in the process to another. To move a gas, a positive pressure or a vacuum must be created. When positive pressure is applied to a standard cubic foot of gas, it gets smaller. Conversely, when a vacuum is applied to a standard cubic foot of gas, it expands. The volume of gas after it is pressurized or rarefied is referred to as its "actual" volume.
Beware that some compressor manufacturers will use the term CFM for the flow of air out of the compressor discharge to the receiver or to the plant air mains. Others will use the acronym ACFM (Actual CFM) as the measure for air from their compressors.
Now we can begin calculating. Here is the equation to convert from SCFM to ACFM, assuming an ideal gas, i.e. Z=1:
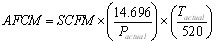 (Equation 2)
(Equation 2)
, where Pactual is in psia and Tactual is in deg R.
Here is the equation to convert from ACFM to SCFM assuming an ideal gas:
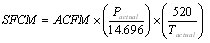 (Equation 3)
(Equation 3)
, where Pactual is in psia and Tactual is in deg R.
Here is the equation to convert from SCFM to ICFM assuming an ideal gas:
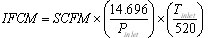 (Equation 4)
(Equation 4)
, where Pinlet is in psia and Tinlet is in deg R.
Example of How to Convert from SCFM to ACFM
In this example, we will find what volume of gas 2,500 scfm represents at 200 psig and 250 deg F. First, make sure to convert gauge pressure into absolute pressure units, i.e., 200 psig = 214.7 psia and temperature into absolute units, i.e., 250 deg F =710 deg R. Now we can readily calculate ACFM using Equation 3 and obtain a value of 233.1 actual cubic feet per minute.
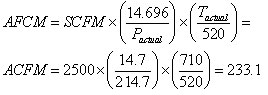
Visualizing Gas Flow
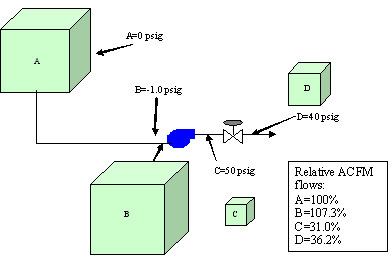
To better understand the relationship between these different flow terms, we will study the simple compression system depicted in Figure 1 (below). Here a compressor takes suction from the atmosphere (standard conditions) and discharges the gas into a higher pressure system of 50 psig. Eventually, the gas flows across a control valve, causing the pressure to drop to 40 psig. If we follow the air flow through the compression system in Figure 1, we can see how each of these flow terms apply.
Here are the basic assumptions:
- Start with 1,000 scfm at standard conditions at Point A
- Then we see a drop in pressure to -1.0 psig (13.7 psia) at the compressor suction at Point B
- Then we see an increase in pressure at Point C to 50 psig.
- Finally we see a drop in pressure to 10 psig at Point D.
Table 1 summarizes the change in volumetric flowrates at these conditions.
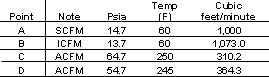
At the entrance A piping, the gas volume is 100 percent. Because there is some pressure drop in the suction piping, the inlet volume (ICFM) at B will be slightly greater (107.3 percent) than the volume at A. After the gas is compressed, the volumetric flow at the compressor discharge, designated as actual cubic feet per minute (ACFM) will be less (31.02 percent) than the volumetric flow at A. Finally, after the control valve, the ACFM increases slightly (36.17 percent) compared to the flow at C because the pressure has been reduced.
With time, these equations will become second nature and the relationships between volumetric gas flow, pressure and temperature will be more understandable. When someone asks how much gas flow is needed, ask them: Do you want the flow in SCFM, ACFM or ICFM?


