Pump designers know that designing a complex pump is easier than designing a simple one. Having my own roots in design, I know how tempting it is to add another feature and a tweak to a pump design. Despite the best engineering intentions, pump designs developed in the comfort of an air conditioned design office often end up a disaster in the field.
Statistics reveal that reliability is an inverse function of the number of components in a machine—doubling the number of parts reduces reliability by half. When applying this simple rule to pumps, a double mechanical seal, for example, makes the entire pump less reliable when compared to a unit equipped with a single mechanical seal.
Another example is adding a feature of external adjustment to the end clearance between the pump and casing. This may be a good selling feature, but it makes a pump more complex and less reliable.
Once the realities of the field kick in, the much-praised double mechanical seals may be replaced by single mechanical seals or eliminated and replaced with packing—a much simpler and more reliable method of keeping most of the fluid out of the pump. As for field-adjustment of the end clearance, most end users reset the clearance during overhauls and not in the field. Modifying the clearance is not pleasant or easy and unwise when surrounded by running machinery, hot pipes, dirty enclosures and poorly lit corners.
Some of these more complex technologies are justified in some applications. Clearly, an 800-degree hot oil pump would not be a good place to apply packings. A highly corrosive acid is not a good natural lubricant for a packed stuffing box, which needs to leak for the packing to remain lubricated. These cases exist but are rare.
For perhaps 80 percent to 90 percent of pumps, the added feature is more a sales ploy than requirement for reliability. This is why mechanical seals are installed on vertical pumps that move clean, or nearly clean, water, when they are not needed. In this process, a $300 packing would work adequately, without the difficulties and the expense of a mechanical seal. Because conducting a field study to correlate the overall expense associated with maintaining pumps and their components is impractical, the result is that end users remain at the mercy of whatever improvement features were included with or added to the pumps.
Because the person who approves a feature may not know how to change a simple packing, impractical add-ons sometimes happen in the field.
An Example
Let’s try to approximately quantify reliability for a simple, end-suction centrifugal pump (see Figure 1).
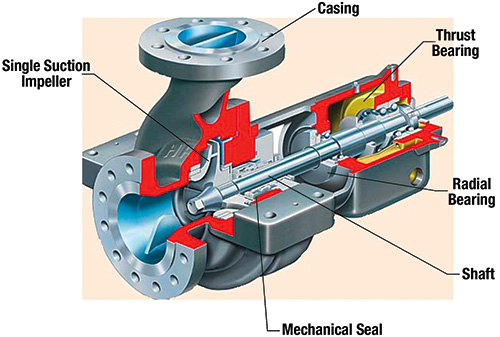 Figure 1. A simple, end-suction centrifugal pump
Figure 1. A simple, end-suction centrifugal pumpNotice that the shaft diameter is smaller as it transitions from the bearing area to the seal area. For simplicity, the shaft is 3 feet long, of which a 1-foot span is between the bearings (assume a 4-inch diameter), and a 2-foot (3-inch diameter) section is an overhung length from the bearing to the impeller. Intuitively, would you not feel somewhat uncomfortable with such a skinny shaft? Well, says the salesman, you need this length … how else can you fit a double mechanical seal? We will calculate the radial deflection of the shaft at the impeller. The basic cantilevered-beam deflection (y) formula is:
y = F x L3 / (3 x E x I)
[Equation 1]
Where:
F = radial load
L = cantilevered length (24 inches)
E = modulus of the elasticity of the material (30,000,000 for steel in our example)
I = moment of inertia
For a circular shaft, I = 3.14 x D4 / 64 (3.98 inches4 in our example), and therefore, a deflection at a given force is proportional to:
y ~ L3 / D4, or abbreviated, it is often written as L3D4
[Equation 2]
The lower that L3D4 is, the less is the shaft deflection, which is better for the seals. If L3D4 becomes too large, a pump shaft can snap, especially if operated close to shutoff, where hydraulic radial loads are excessive. American National Standard Institute (ANSI) pumps, for example, have L3D4 ratios range from 20 to 120.
The value of the radial load depends on many variables—such as a type of volute, operating point (percent of best efficiency point) and other factors beyond the limits of this article—but for this design, a 2,000-pound load is a reasonable estimate for this example:
y = 2,000 x 243 / [3 x 30,000,000 x 3.98] = 0.078 inch
[Equation 3]
What would happen if we shorten the shaft by half (see Equation 4)?
y = 2000 x 123 / [3 x 30,000,000 x 3.98] = 0.009 inch
[Equation 4]
Equation 4 results in an order of magnitude reduction in deflection. The L3D4 factor went from 243 / 34 = 171 to 123 / 34 = 21.
How will a reduction in shaft deflection affect pump life?
Can/should the shaft be shortened by half? If this is done, at what compromise and at what price? Tell us, and the best answer will appear in a later issue of Pumps & Systems.


