Why do those three affinity laws do such a good job of predicting the performance of a centrifugal pump when its rotational speed or impeller diameter is changed? Well, it turns out that they are not just guesses or approximations. They are actually rooted in the work of Isaac Newton, whose laws of motion also debunk the myth of centrifugal force.
Let’s take a look at how an impeller adds energy to a fluid and why that energy change can be predicted by the affinity laws.
Adding Energy
Energy can exist in many different forms, but in the centrifugal pump it is added by increasing the velocity of the incoming fluid. As an impeller rotates, fluid enters the vanes at its eye and is accelerated to some maximum velocity just as it exits the vanes at its periphery. Since the exit velocity of the fluid is greater than its inlet velocity, there is a net increase in energy within the pump, and this additional energy results in increased pressure and flow.
Now some would have you believe that this acceleration is due to a “center fleeing” component known as centrifugal force. But you have to take this with a grain of salt because if this force did exist, a ball swinging in a circle on a string would fly outwards from the point at which it is released (see Figure 1). In real life, the ball travels in a straight line that is tangent to the circle.
In other words, it travels in the very same direction it was traveling at the instant it was released. I use this same demonstration in my lectures and classes. If you are not convinced, give it a try yourself.
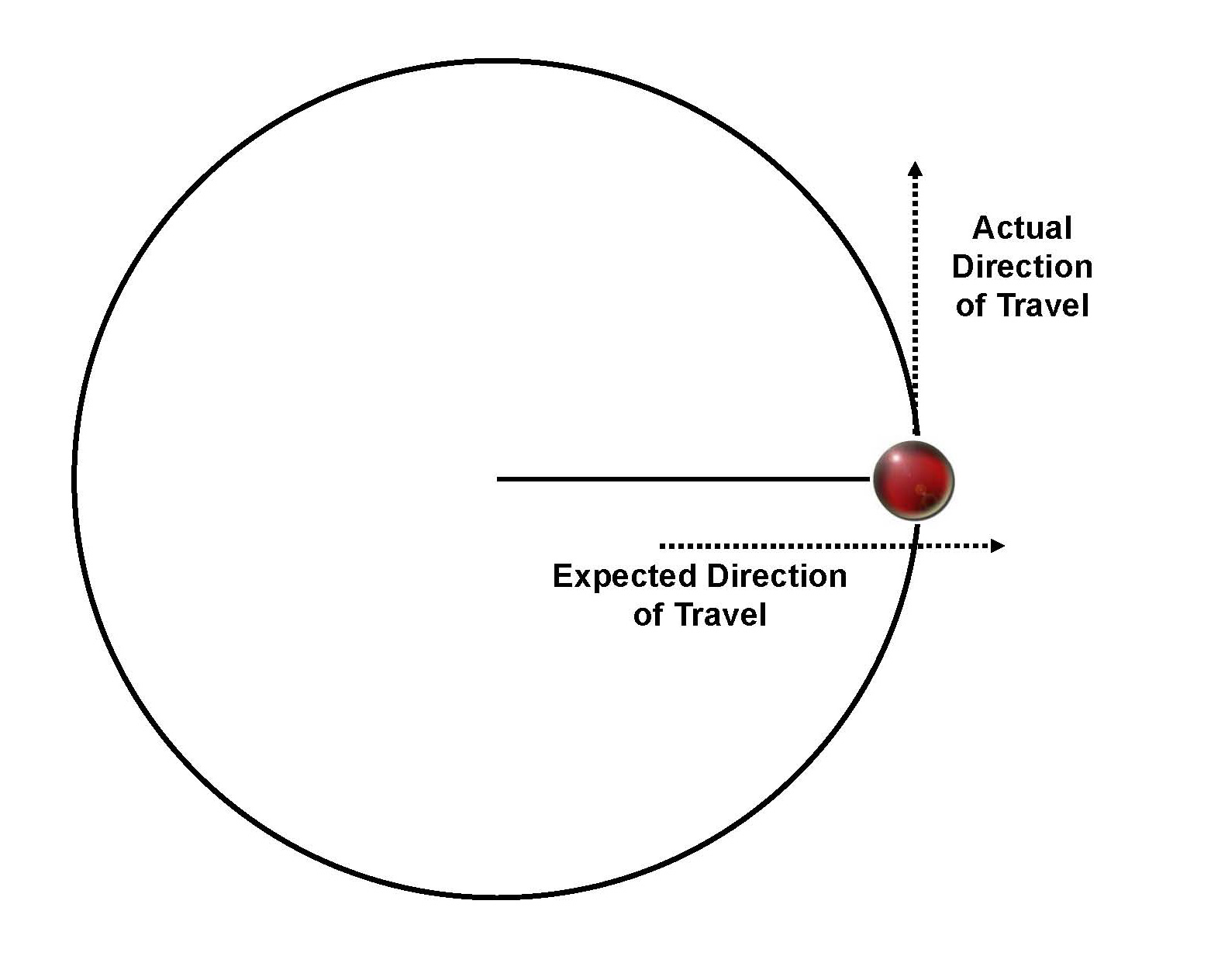
Figure 1
Centrifugal force is one of three false, or apparent, forces found in nature. Its “apparent” existence is totally based upon one’s frame of reference. For example, if you round a sharp curve at high speed you will feel a force that seems to pull you toward the outside. But that pull is really the result of your body trying to obey Newton’s first law of motion and, in doing so, maintain its original direction of travel and velocity.
So if centrifugal force really is a farce, how is that energy of velocity added by the impeller?
Actually, it’s pretty simple, but sometimes our brains have a difficult time visualizing distance and speed when they occur in a rotational environment. Figure 2 shows an impeller that has a diameter of 12-in (radius of 6-in) and a circumference of 3.14-ft. If the impeller completes one rotation each second, a point on its periphery will travel a distance of 3.14-ft at an equivalent linear velocity of 3.14-ft/sec.
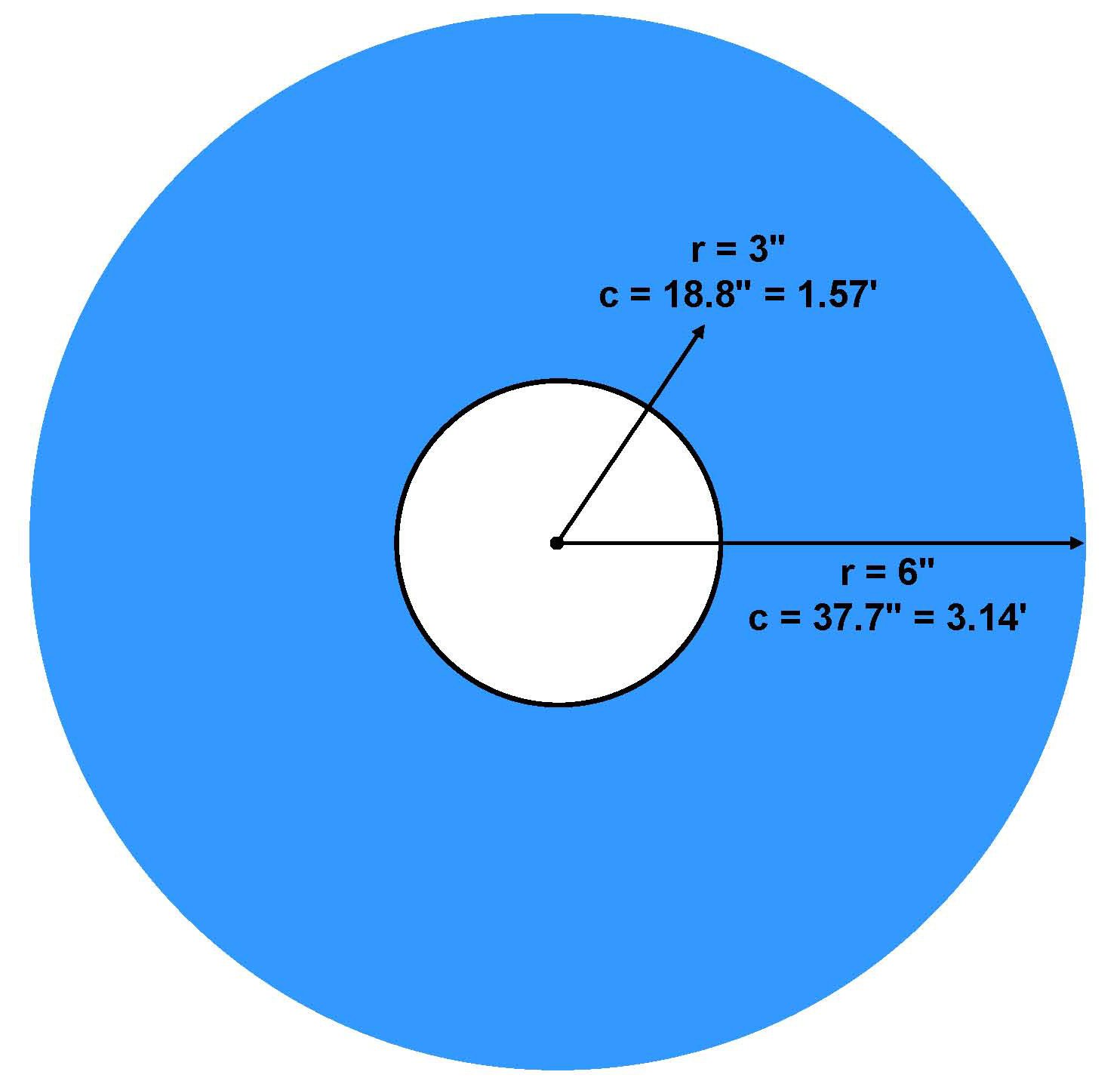
Figure 2
Now, let’s take a look at a point that is halfway (3-in) between its center and periphery. Here we calculate a circumference of 1.57-ft. The point at 3-in is still traveling at one rotation per second, but the distance it travels is just half that of the point at 6-in. Therefore its velocity must also be half that of the point at 6-in.
As a fluid is guided through the impeller vanes, it encounters an ever-increasing radius and its velocity will be proportional to the circumference at any given point on that radius. In our example, the fluid velocity would be small as it enters the impeller eye, but would increase to 1.57-ft/sec halfway down the vanes and exit the vanes at 3.14-ft/sec.
In this simple manner, an impeller adds the energy of velocity to a fluid. The maximum (peripheral) velocity it can attain is dictated by a combination of impeller diameter and rotational speed. Reduce the diameter or rotational speed and you reduce peripheral velocity.
Now, the velocities above are quite small because our rotational speed was just one rotation per second, or 60-rpm. At a more typical 1750-rpm, those 3-in and 6-in velocities will increase to 45.8-ft/sec and 91.6-ft/sec, respectively. Now that we know how energy is added by the impeller, let’s take a look at how the affinity laws are able to predict its effect on flow, head, and power.
Affinity Laws – The Power of 1, 2, & 3
The first law is all about velocity. It states that flow is directly proportional to a change in speed. When we say that some variable changes in direct proportion to another, we are saying that the changes are equal. If X changes by 50 percent, Y will change by the same amount. So if we reduce an impeller’s rotational speed by one-half, the flow through its vanes also reduces by one-half.
If a piston pump can displace one gallon per stroke and performs sixty strokes each minute, its flow rate is 60-gpm. Reduce that to 30 strokes and its flow reduces to 30-gpm. The centrifugal pump operates in a similar manner, but it is the fluid’s velocity – not mechanical displacement – that causes flow. Like the piston pump’s cylinder, the impeller has some defined internal volume, and the number of “impeller volumes” that exit the vanes (per unit of time) is totally dependent upon the velocity of the fluid within those vanes. If we alter that velocity by changing rotational speed, flow is altered by the same amount.
The second law is also about velocity. It states that head varies as the square of a change in speed. When we say that variable A changes as the square of variable B, we are saying that the change in A is equal to the change in B multiplied by itself. So if we reduce speed by one-half, the resulting head is reduced to just one quarter of its original value (½ x ½ = ¼). But where did the square come from?
Well, it turns out that quite a few things in nature follow this square rule. For example, wind resistance (or drag) changes the square of a change in speed. That is why your car’s gas mileage is lower at 70-mph than it is at 50-mph, even though the engine efficiency is about the same. But that still doesn’t answer the question. Well, would you believe that it follows the same rule as falling water?
The equation v2 = 2gh is often referred to as the falling body equation. It can be used to calculate the speed at which some object (water included) will strike the surface of the earth when falling from some height (h) in the absence of air resistance (g is the universal gravitational constant at 32-ft/sec/sec). If we rearrange this equation (h = v2/2g), we can also calculate the height an object will attain based upon some initial velocity.
As you can see, height changes as the square of a change in velocity. Double the velocity and height increases by four times. Reduce the velocity by one-half, and height reduces to one quarter of its original value. The head produced by a centrifugal pump is dependent upon its peripheral (initial) velocity and it is governed by this same simple equation.
The third law is simply a product of the changes we saw in the first two laws. It states that horsepower varies as the cube of a change in speed. In a cubic relationship, the change is multiplied by itself and the resulting product is again multiplied by the change. If we reduce speed by one-half, horsepower is reduced to one-eighth of its original value (½ x ½ = ¼ x ½ = 1/8).
In order to see why this happens, we have to convert horsepower into a more basic unit of work. In the English system, 1-hp is equal to 33,000-lbft/min (or ftlb if you are over 50). Let’s take a look at a simple example. Suppose we have a pump that can produce 100-gpm at a head of 100-ft when running at full speed. At half speed, the first two affinity laws will dictate a flow of 50-gpm and a head of 25-ft. Now, let’s convert flow and head into lbft/min and calculate the horsepower required at full and half speed.
100-gpm x 8.35-lb/gal x 100-ft =
83,500-lbft/min ÷ 33000-lbft/min = 2.53-hp
50-gpm x 8.35-lb/gal x 25-ft =
10,437-lbft/min ÷ 33000-lbft/min = 0.316-hp
These simple calculations show the theoretical horsepower (assuming 100 percent hydraulic efficiency) required to pump water at full and half speed, and their results support the prediction of the third law. Note that 0.316 is, in fact, 1/8 of 2.53. The reason this relationship varies in this manner is because the pounds pumped per unit time is only one-half that of full speed, and the elevation to which they are pumped is but ¼ of the original head. And in very simple math, 1/2 x 1/4 = 1/8.
Pumps & Systems, September 2006

