First of Two Parts A primary objective in any pump installation should be to minimize loads on a pump induced by the piping system design. Piping in the vicinity of the pump should be properly supported and restrained to obtain optimal pump service life. If this is not accomplished, objectionable loads can be placed on the pump that can reduce the service life of the equipment, increase maintenance costs and the total cost of ownership of the pump or result in catastrophic pump failure. Piping loads placed on a pump will be transferred through the pump to the pump support structure and the foundation under the pump. If the loads are high enough, foundation problems can also occur. In terms of load-carrying capability, pumps are a relatively weak element. Their capability is not comparable to piping, piping restraints or pipe anchors. Excessive loads can overstress and distort the pump casing, causing relatively tight internal clearances to be overcome and creating excessive misalignment with the driver. In severe cases, the piping loads can crack the pump casing. Proper piping-pump interaction is not automatic, so users should analyze piping loads to ensure that the pump's load capability is not exceeded. If the piping system design is carefully engineered, users can practically eliminate or manage piping loads to avoid these troublesome scenarios in most installations. The piping near the pump must be carefully evaluated. A system designer should recognize that pump piping loads fall into three categories:
- Residual mechanical pipe strain forces
- Hydraulic pressure reaction forces
- Thermal growth or contraction reaction forces
Mechanical Pipe Strain Forces
Mechanical pipe strain caused by piping misalignment and piping excessive assembly tolerances is the easiest source of piping loads to visualize. A reasonably precise pump and piping installation will prevent such loads. Piping flanges bolted to pumps should be close to the pump flange in their unbolted position so excessive force is not required to pull the flanges into the operating position. In general, the separation of the unbolted pipe flange from the pump flange should be within a small tolerance of the gasket thickness. In any case, a flange separation amount is excessive if it results in the pump flange moving some amount in line with the pipe when the flanged joint is unbolted. For small pumps, 0.005 inches is a good worst-case limit criterion and will be used throughout this article. Piping flanges bolted to pumps should also be relatively parallel to the pump flange in their unbolted position. A tolerance of 0.001 inches per inch of flange outside diameter with a maximum of 0.010 inches typically ensures that the as-installed piping misalignment will not place undue stress on the pump. Because forces from other potential sources will be present, mechanical pipe strain loads should be kept low. The effects of the fluid mass are often overlooked. If the piping is not properly supported, piping that is aligned with the pump in the dry state can move and improperly load the pump when the system is filled and prepared for service.Hydraulic Pressure Reaction Forces
Pressure in a pipe causes expansion of the pipe, even if only a small amount, in all directions. Linear expansion is caused by the pressure acting on the projected area of the pipe corresponding to the pipe's inside diameter. If valves or special pipe fittings with larger inside diameters than the pipe are present, the area corresponding to the maximum inside diameter should be considered. This often involves a much larger area than the pipe and a much larger force. Figure 1 illustrates this by using a rubber expansion joint as an example.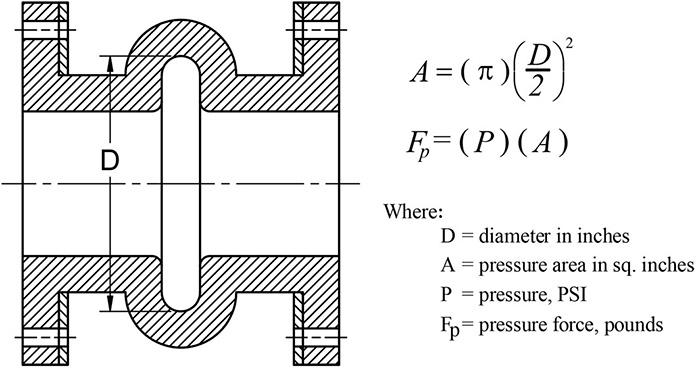 Figure 1. Rubber expansion joint (Graphics courtesy of Patterson Pump Company)
Figure 1. Rubber expansion joint (Graphics courtesy of Patterson Pump Company)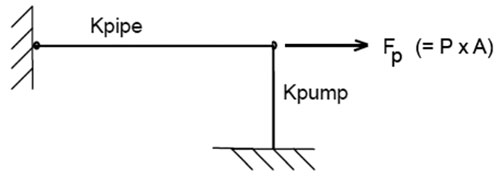
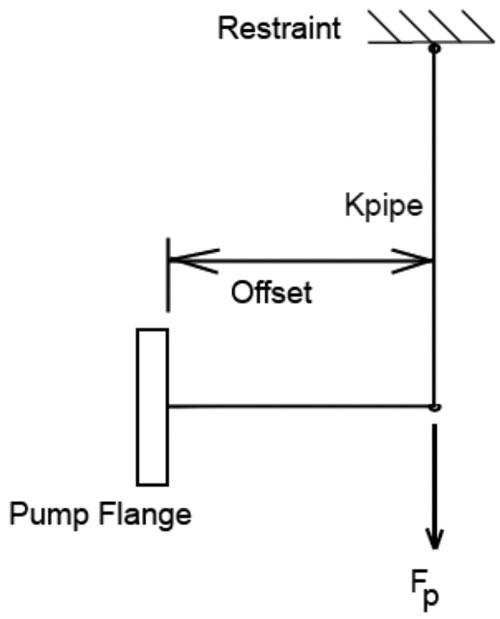
- The hydraulic pressure force is easily constrained by thrust rods and easily transmitted to the piping that can handle such force.
- The hydraulic pressure reaction loads placed on the pump in such cases are typically relatively high compared with the pump capability.
- Any hydraulic pressure reaction force placed on the pump is transmitted to the support structure and foundation.
- A hydraulic pressure reaction force will load the pump, support structure and foundation each time the pump is started.

