Inexperienced vibration analysts encounter a common problem: They are often expected to learn too much, too fast. Instead of taking time to appropriately understand the basics, new analysts must often move directly to a busy schedule of collection and analysis without much apprenticeship. Training is almost always in a group setting, and instructors often move too quickly through the material. The facts are learned well enough for an analyst-level exam, but an in-depth understanding is often taken for granted. Accurate vibration analysis requires complete clarity on foundational subjects. Real-world applications demand more of young analysts than what they can learn in group training. Facility operations depend on a whole picture of how their equipment moves and where energy is used—and lost.
Configuring Data Collection Parameters
Good data requires correct placement of the proper transducer. The data collector must be properly configured to collect the necessary maximum frequency in the spectrum (fmax) and resolution of data. A data collector device is only as good as its user. It will only do what the analyst tells it to do. Many companies buy data collection equipment without understanding this fact. That is why they spend thousands buying the equipment, but spend little training its user. The most basic objective for an analyst in training is to obtain data that will reveal the probable defects in a particular machine and have enough detail to discriminate between them. The data must include a high enough fmax to capture the data and reveal the faults that cause higher frequency vibrations. At the same time, it must have enough resolution to reveal the true cause of the fault or defect. The spectrum in Figure 1, taken at the inboard horizontal of a motor, shows many multiples of turning speed, which indicate looseness.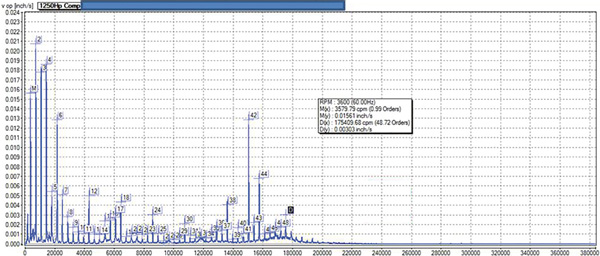 Figure 1. An FFT spectrum (Graphics courtesy of LUDECA, INC.)
Figure 1. An FFT spectrum (Graphics courtesy of LUDECA, INC.)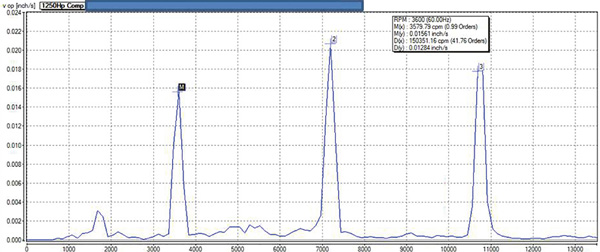 Figure 2. A magnification of the 1x to 3x peaks
Figure 2. A magnification of the 1x to 3x peaks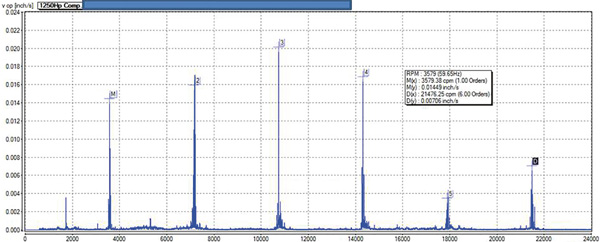 Figure 3. A higher-resolution FFT analysis
Figure 3. A higher-resolution FFT analysis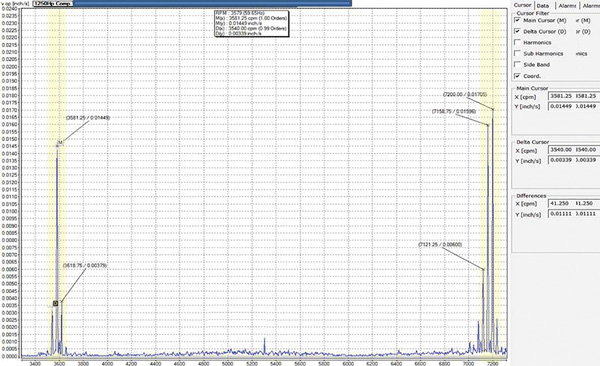 Figure 4. A zoomed-in view of the higher-resolution FFT analysis
Figure 4. A zoomed-in view of the higher-resolution FFT analysisUnderstanding Resolution
Analysts can fundamentally understand resolution by relating it to time. Higher-resolution data takes more time. Figure 5 is a 0.5-second time waveform (twf). Remember, 500 milliseconds equals 0.5 seconds. This twf is used to calculate the lower-resolution fft analysis in Figure 1. Equation 1 may be used to find the resolution, but looking at it purely from a time perspective gives a better idea of its simplicity. Figure 5. A 0.5-second twf
Figure 5. A 0.5-second twf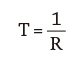 Where:
T = Time
R = Resolution
Figure 6 takes this 0.5-second twf and puts it on a time line of 2 seconds. The line begins at 0.75 second and ends at 1.25 seconds.
Where:
T = Time
R = Resolution
Figure 6 takes this 0.5-second twf and puts it on a time line of 2 seconds. The line begins at 0.75 second and ends at 1.25 seconds.
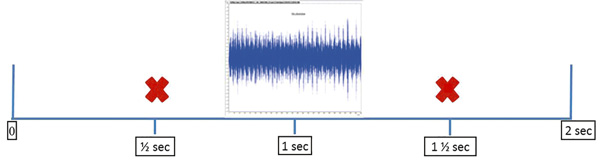 Figure 6. A 0.5-second twf on a 2-second time line
Figure 6. A 0.5-second twf on a 2-second time lineLOR & fmax
What about fmax and lines of resolution (LOR)? The resolution was determined by dividing time by one. However, most data collectors and software do not allow the user to specify fmax and resolution. An analyst needs to know that fmax divided by LOR equals the maximum possible resolution (see Equation 2). Remember, the lower-resolution fft had an fmax of 384,000 cpm and 3,200 LOR. Equation 2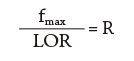 Where:
fmax = Maximum frequency in the spectrum
LOR = Lines of resolution
R = Maximum resolution possible
Where:
fmax = Maximum frequency in the spectrum
LOR = Lines of resolution
R = Maximum resolution possible
 An fft connects the dots between LORs, where each line is a dot of data. Figure 7 shows a zoomed-in view of the 1× of the lower-resolution fft. Each LOR is a bin of data—one number representing an average of the vibrations recorded at that frequency. The number represents a dot in the center of that bin. The software draws the fft without showing the dots.
An fft connects the dots between LORs, where each line is a dot of data. Figure 7 shows a zoomed-in view of the 1× of the lower-resolution fft. Each LOR is a bin of data—one number representing an average of the vibrations recorded at that frequency. The number represents a dot in the center of that bin. The software draws the fft without showing the dots.
.jpg) Figure 7. A zoomed-in view of the 1x peak of the lower-resolution FFT
Figure 7. A zoomed-in view of the 1x peak of the lower-resolution FFT
