The Bernoulli Principle

Read Part One

Read History of Pumps series

The Bernoulli Principle explains the flow of fluids and was one of the earliest examples of conservation of energy. It states that during steady flow, the energy at any point in a conduit is the sum of the velocity head (v), pressure head (P) and elevation head (z). It takes the form of a conservation equation where the sum of the three variables will always remain constant as long as no losses or additions occur.

Energy = v + P + z = Constant

In the example below, Bernoulli’s equation is expressed in terms of pressure or force per unit area. The first term is dynamic pressure, which is a result of the fluid velocity and its density. The second is hydrostatic pressure, which is due to any changes in elevation. The third is static pressure, which is the actual thermodynamic pressure relative to flow. The sum of the three equals the total pressure. Total pressure will remain constant as long as energy is not added or removed from the system.

1/2ρv² + ρgz + P = P_total = Constant

Where:
ρ = density
v = flow velocity
P = pressure
g = acceleration due to gravity
z = elevation

Bernoulli’s equation can also compare the pressures at any two points in a flowing conduit. Once again, if no energy is added or lost, the sum of the three terms on the left will equal the sum of the terms on the right.

(1/2ρv_a² + ρgz_a + P_a) = (1/2ρv_b² + ρgz_b + P_b)

Where:
a and b are at different locations within the conduit

Bernoulli’s Theory in Action

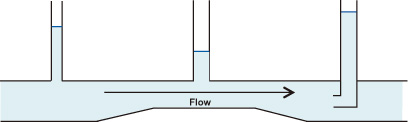
Figure 1 shows the Bernoulli Principle in action. It is similar to the one demonstrated in Part 1 of this series (“The Life and Work of Daniel Bernoulli,” Pumps & Systems, August 2012). Here, a horizontal pipe flows continuously from left to right with no energy losses due to friction. The left and right have diameters that are the same, but the portion in the center is just two-thirds as large. The vertical tubes (piezometers) to the left and in the center are vented to atmosphere, and their water levels are proportional to the static pressure in those areas. They measure static pressure in the same way as a pressure gauge. Note that the measured pressure in the larger diameter portion is greater than that of the constricted portion. This would be expected since velocity is obviously higher in the center section. Bernoulli’s equation tells us that pressure decreases as velocity increases.

Figure 1. A horizontal pipe that flows continuously from left to right with no energy losses due to friction

 

However, something seems strange about the pressure indicated by the water level in the vertical tube on the far right. One would expect the pressure to return to that of the far left piezometer if there are no losses due to friction in the constricted area. But its level indicates a higher pressure, and no additional energy was added to the system. It turns out that the column on the right is a Pitot tube. This device measures pressure in a different way. In addition to static pressure, it also measures the additional pressure created by the flow velocity.

If a valve on the downstream side were closed and flow ceased, all three vertical tubes would measure the same static pressure, regardless of their locations and shapes. Once flow is resumed, the static pressure, measured by the piezometers, will be the static pressure in that particular area. However, unlike the piezometer, the entrance of the Pitot tube faces upstream and allows the flow to push more water into the tube. When water ceases to flow into the tube (stagnation), its vertical level is at its maximum and is equal to the sum of the static and dynamic pressures. The pressure measured by the Pitot tube is the total pressure in the flowing conduit.

Figure 2 is a graphical representation of the Bernoulli equation. It is often used during the design of pipelines and open channel systems. It can be used to show the effect on a hydraulic system due to changes in pipe size, elevation, pressure, and fitting and valve losses. This example illustrates the pressure at three points in a pipe that is undergoing steady, continuous flow with no changes in elevation.

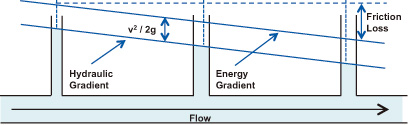Figure 2. A graphical representation of the Bernoulli equation

 

The water levels in the vertical pipes are the static pressures at those points. The angled line connecting them is called the hydraulic gradient or hydraulic grade line. The angled line above that parallels the hydraulic gradient is the energy gradient and represents the total pressure in the pipeline. It can be measured by a Pitot tube, or it can be calculated using the flow velocity and the equation for velocity head (v2/2g).

The energy gradient or grade line is the sum of the velocity head and the static pressure at any point. In this example, velocity head remains constant at each point, but static head is reduced based on the total friction at each point. In more complex examples, these two gradients would not parallel one another but would move in both directions depending on the pipe size, elevation and other factors.

The Bernoulli Principle is in action when an airplane flies or a baseball curves. His principle also holds true at sea. The reason that ships must not pass too closely is that the increased velocity of the water passing between them creates a low pressure area that can cause a sideways collision. For this reason, large docks tend to have pilings rather than solid walls. Lastly, there is the “shower curtain” effect.

In a future article, we will investigate some similar work performed by Giovanni Venturi and Evangelista Torricelli and how their work, too, advanced our understanding of hydraulics. Next month, we will illustrate the importance of accounting for velocity head when testing pumps in the field.