In part one of this two-part column, we will define water hammer and explore the events that cause it. We will also try to gain perspective on the additional pressure it generates. To read part two, click here.
What is water hammer?
Water hammer (also waterhammer) is a pressure surge that can arise in any pumping system that undergoes an abrupt change in its rate of flow and usually results from pump starts and stops, the opening and closing of valves, or water column separation and closure. These abrupt changes can cause all or part of the flowing water column to undergo a momentum change. This change can produce a shock wave that travels back and forth between the barrier that created it and a secondary barrier. If the intensity of the shock wave is high, physical damage to the system can occur. Oddly enough, water hammer can be more of a concern in low pressure applications.
Water hammer is yet another example of conservation of energy and results from the conversion of velocity energy into pressure energy. Since liquids have a low compressibility, the resulting pressure energy tends to be high.
Perhaps the best way to visualize water hammer is to start with a hypothetical example. Figure 1 below shows a pump pumping water into a pipe that was empty when the pump started. The two valves, located at the pump discharge and the far end of the pipe, are fully open and have the ability to close instantaneously. The pipe, valves and other fittings are entirely inelastic and no volume change can occur, regardless of the pressure. The column of water flowing through the pipe also has a perfectly flat leading edge that matches that of the cross sectional ID of the pipe. When the leading edge of the water column reaches the downstream valve, it closes at nearly the speed of light and entraps no air ahead of the water column.
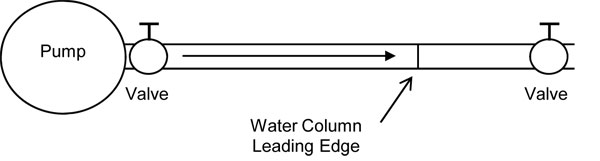Figure 1Even though the leading edge has struck the closed valve, flow into the pipe continues for the next few milliseconds. Just as flow ceases, the upstream valve closes (this time at the true speed of light), and the water column is completely isolated between the two valves. What events occur as the column strikes the closed, downstream valve and why does water continue to enter the pipe even though the valve is closed?
If this moving column was a column of metal instead of water (hypothetically, of course), a couple of things could occur. Depending on its coefficient of restitution (its ability to avoid permanent damage), the kinetic energy due to flow (motion) could be transformed into mechanical energy as the leading edge of the metal column is crushed against the closed valve. If this occurred, the column would come to rest and remain motionless at the valve. If its restitution is high enough to prevent crushing, that same kinetic energy could be used to reverse its direction in the form of a bounce. Regardless of the outcome, the "entire" metal column would either come to rest or bounce in the opposite direction. Neither of these events occurs when water is involved.
Water is a nearly non-compressible liquid, which seems to suggest it is slightly compressible. At ambient temperature, 1-psi will decrease its volume by about 0.0000034 percent. That seems pretty small, but the larger the volume, the easier it is to see the effect. For example, if water did not compress, sea level would be roughly 100-ft higher than its current level! At very high pressures, say 40,000-psi, its compressibility is increased to about 10 percent. But, most water is not just water-it also contains air, which is primarily nitrogen (78 percent) and oxygen (21 percent). Otherwise, fish could not survive! Dissolved air composes about 2 percent of a given volume of unprocessed water, and adds substantially to its compressibility.
Why
It is water's (and dissolved air's) compressibility that causes water to act differently than the metal column. Were it not compressible, its leading edge would be permanently crushed or the entire column would bounce backward. When the leading edge of a water column strikes the closed valve it abruptly stops. Since the water behind the leading edge is still in motion, it begins to compress. This compression along the entire length of the column allows a small amount of water to continue to flow into the pipe even though the leading edge has halted. When flow ceases, all of its kinetic energy of motion and that due to compression is converted into pressure energy.
Compression begins at the leading edge of the water column and since the additional energy it produces cannot continue past the closed valve, a pressure or shock wave is generated and travels along the path of least resistance which, in this example, is back upstream. Its inception is similar to the echo produced when a sound wave, traveling through air, strikes a similar barrier. When the wave hits the upstream valve, it is reflected back downstream but with a diminished intensity. This back and forth motion continues until friction and reflection losses cause the wave to disappear. The speed at which a wave travels and the energy it loses during travel depends on the density and compressibility of the medium in which it travels. The density and compressibility of water make it a good medium for shock wave generation and transmission.
The pressure waves created by hydraulic shock have characteristics similar to those of sound waves and travel at a similar velocity. The time required for a water hammer pressure wave to negotiate a length of pipe is simply the pipe length divided by the speed of sound in water (approximately 4,860-ft/sec). In water hammer analysis, a time constant that is often used describes the progression of the wave from its inception to the secondary barrier and then back again. It takes the form of Tc = 2L/a (where L is the pipe length and a is the velocity of the wave, which is the speed of sound). In a 1,000-ft pipe, the wave can make a complete round trip in less than one half second.
The pressure created by this shock wave is directly proportional to both the wave velocity and the velocity of the water flowing in the pipe. Although the equation below does not take into account the effect of pipe length, diameter and elasticity, it will provide some insight as to the additional pressure created by a water hammer pressure wave.
P(additional) = aV / 2.31g
P is the additional pressure the shock wave creates, a is wave velocity, V is the velocity of the flowing water in the pipe in feet per second, g is the universal gravitational constant @ 32-ft/sec2 and 2.31 is the pressure conversion constant. At a pipeline velocity of 5-ft/sec², the additional pressure created by the shock wave is approximately 328-psi. Increasing that velocity to 10-ft/sec increases the additional pressure to about 657-psi. Obviously, systems that are not designed to accommodate such an increased pressure are often damaged or even destroyed.
Next month we will explore the three major causes of water hammer and the factors that contribute to the magnitude of the shock wave it generates. We will also see why water hammer can be more damaging in low pressure systems.
