Do Pumps Require Less NPSH on Hydrocarbons?
Yes.
The extensive application of pumps to hydrocarbon services in the first half of the 20th century produced numerous observations that centrifugal pumps handling liquid hydrocarbons were able to operate satisfactorily with less NPSH available than when pumping water, and the NPSHR was less when pumping lighter hydrocarbons than when pumping heavier hydrocarbons.
Based on tests and field observations, the Hydraulic Institute (2) and the Natural Gas Processors Suppliers Association (3) published correction factors (based on suction pressure and the specific gravity of the pumpage) to use as multipliers for water NPSHR.
Stahl & Stepanoff (4) expanded understanding of the subject by investigating NPSHR from the standpoint of the thermodynamic properties of the pumpage, proposing the reason for hot water NPSHR being less than cold water NPSHR, and suggesting that 70deg F propane would have the same NPSHR as 300 deg F water.
Salemann (5) performed NPSH tests on water, butane, benzene, kerosene, gasoline and Freon‑11 at various temperatures, showing the correction to cold water NPSHR not as a factor, but as a fixed head subtraction.
Whistler (6) explained the reason for the different NPSHR when pumping various liquids, and confirmed that the reduction in NPSHR was not a factor, but a fixed head (in feet or meters) to be subtracted from the (cool) water NPSHR. His equation, which can be used to calculate the NPSHR correction from thermodynamic properties, is as follows:
Δh = (2.31/SGL)[(P1-P2)/(T1-T2)](V)(SGV/SGL)(F + H/100Cp)
Where (in U.S. units):
Δh = Subtraction from cool‑water NPSHR, ft
SGL = Specific gravity of liquid
SGV = Specific gravity of vapor (relative to water)
(P1-P2)/(T1-T2) = Slope of vapor pressure curve, psi/deg F
V = Volume percent of vapor to liquid in imp. eye
F = Slope of initial vaporization, deg F/wt. % vapor
H = Latent heat of vaporization, BTU/lb
Cp = Specific heat of liquid, BTU/lb‑deg F
V is the percent volume of vapor in the impeller eye to produce a 3 percent head drop. Whistler suggests two as a reasonable number. If the pumpage is a single component, F = 0.
The Hydraulic Institute (2) and NGPSA (3) subsequently replaced their factor charts with a chart that provided a fixed correction to NPSHR, based on pumpage thermodynamic properties. Those charts indicate a larger V factor than the two suggested by Whistler.
With great 20‑20 hindsight, we can now explain this phenomenon.
As stated earlier, the NPSHR for a centrifugal pump is defined as the amount of NPSHA when the head drops 3 percent. The head drops because a certain volume of gas has formed in the impeller eye. Liquids that are closer to their critical pressure will flash to a smaller volume of gas, because the density of the gas is closer to the density of the liquid. A liquid right at its critical pressure could all flash to a gas without affecting pump head (or anything else). (There would actually be no flashing.)
At ambient temperatures, hydrocarbons are closer to their critical pressures than cool water. For the same drop in suction pressure below vapor pressure, less volume of hydrocarbon gas is liberated. Therefore, to get the same 3 percent head drop with the hydrocarbon, the suction pressure must be reduced farther below vapor pressure, so less NPSH would be available, i.e., NPSHR would be less.
Exercise care in applying any correction, though, because hydrocarbons that have their vapor pressures below atmospheric pressure, and are therefore generally stored in atmospheric vessels, will absorb air. The dissolved air will increase the vapor pressure of the solution and will flash out of solution at a pressure above the vapor pressure of the air-free liquid. Although this flashing does not result in cavitation damage to pump components, it can cause a drop in head and erratic pump performance.
API 610 does not allow use of any "hydrocarbon correction" for NPSH, letting any lower degree of cavitation result in less than the 3 percent head drop.
Stepping NPSHR to Different Speeds
Although much has been written stating that it does, the NPSH requirement of a centrifugal pump, based on a 3 percent head drop, does not vary as the square of the speed as the head does. At the BEP (best efficiency point), the NPSHR varies as the speed-ratio to approximately the 1.5 power for the conventional 3 percent head‑drop criterion.
NPSH2 = NPSH1 (N2/N1)1.5
This relationship normally exists only at the BEP. At half the BEP, the exponent is usually about one. At 1.3 x Qbep, the exponent is usually about two.
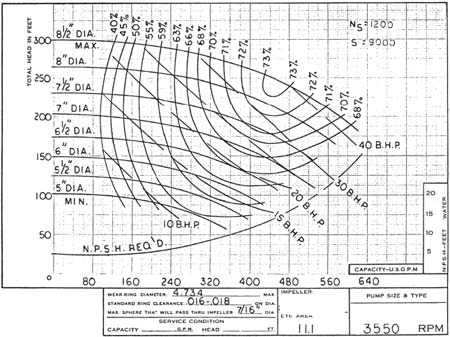
Problem No. 1: Stepping NPSHR to a Different Speed
The performance curve in Figure 2 from Part Four (P&S, May 2009-reprinted below) is for 3,550 rpm. Calculate the approximate NPSHR, for 1,750 rpm, at the BEP. NPSH2 = NPSH1 (N2/N1)1.5 = 14 (1750/3550) 1.5 = 14 (0.346) = 4.8 = ABT 5 FEET (This 5 ft NPSH requirement would be at the 1,750 rpm BEP of about 225 gpm.)
|
Although the above 1.5 exponent is based on the author's experience with centrifugal pump NPSH tests at different speeds, Fang (7) reported different findings (varying exponents). Some continue to use the traditional two exponent (instead of 1.5).
This author concludes that the exponent would be two if NPSHR were based on incipient cavitation, but the 1.5 is more accurate for stepping NPSHR based on the more common 3 percent head‑drop NPSHR.
This characteristic (the 1.5 exponent) has caused significant field problems (1, 8). High energy pumps, tested at the higher speeds, indicate lower NPSH3 than that obtained by stepping the NPSHR3 from a lower test speed using the traditional two exponent. The 40 MW (54,000 hp) boiler feed pump described in reference (9) was NPSH tested at 1,490 rpm, and the results were extrapolated to the 4,620 rpm rated speed using an exponent of two.
Such a procedure eliminates the potential problem created by testing at the high rated speed. Incipient cavitation was observed to occur at an NPSHA about two times NPSHR3. In the plant, a 1,320 rpm booster pump provides NPSH almost three times the extrapolated NPSHR3.
References
1. Vlaming, D. J., "Analysis of Cavitation Provides Advanced NPSH Estimates for Centrifugal Pumps," Oil & Gas Journal, November 19, 1984.
2. Hydraulic Institute Standards, Hydraulic Institute, 6 Campus Drive, First Floor North, Parsippany NJ, 07054-4406.
3. Engineering Data Book, Natural Gas Processors Suppliers Assoc., Tulsa, OK, 1966.
4. Stahl, H. A. & Stepanoff, A. J., "Thermodynamic Aspects of Cavitation in Centrifugal Pumps," ASME Paper No. 55‑A‑136, 1955.
5. Salemann, Victor, "Cavitation and NPSH Requirements of Various Liquids," ASME Paper No. 58‑A‑82, 1958.
6. Whistler, A. M., "A Yardstick for NPSH Requirements," Petroleum Refiner, Jan. 1960.
7. Fang, Ken‑Shou, "How Accurate are Predictions of Required NPSH When Based on Speedscale Effect?", Power, February 1979.
8. Ross, Robert R., "Theoretical Prediction of NPSHR for Cavitation Free Operation of Centrifugal Pumps," United Centrifugal Pumps, about 1982.
9. Elsässer, Thomas; Brecht, Bernhard; Baumgarten, Sven, "The Gentle Giant of Niederaussem," Pumps & Systems, December 2006 (and letters to the editor, February 2007).