Use a mathematical model that estimates vibration at the top bearing of a motor used on a vertical, wet-pit, column type pump.
03/20/2014
First of Two Parts. Find Part 2 here.
"Top-of-Motor Vibration” in the September 2012 issue of Pumps & Systems provided a mathematical model for estimating vibration at the top bearing of a motor used on a vertical, wet-pit, column type pump (see Figure 1)—a topic that continues to interest vertical pump users, specifiers and manufacturers. The simplified cantilever beam model aids in understanding vertical pumps’ vibration and allows comparisons to empirical data for the development of standard vibration acceptance criteria at the top motor bearing, for which no guidance currently exists. Part One of this series discusses insights that may be gained by analyzing the mathematical model.
The structure consists of a motor mounted on a pump discharge head, above the baseplate. As background information, a list of the simplifying assumptions for the mathematical model is provided below:
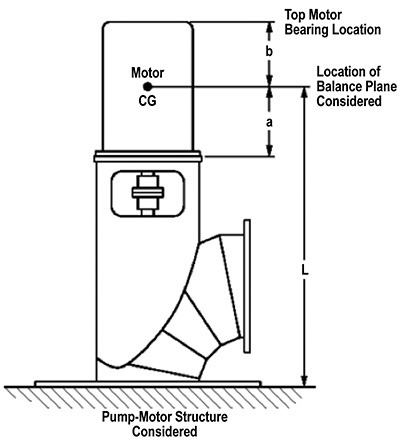 Figure 1. Vertical pump and motor
Figure 1. Vertical pump and motor- The structure of interest is above the baseplate of a vertical, wet-pit, column type pump.
- The focus is vibration at the top motor bearing because of motor imbalance.
- The imbalance acts in a single horizontal plane located at the motor rotor center of gravity (CG) of location.
- The CG of the motor is in the same horizontal plane as the motor rotor CG.
- Only filtered vibration at the operating speed is considered.
- Only the motor mass is considered.
- An infinitely rigid foundation was implied because no foundation effects were considered in the model.
- The natural frequency considered is the reed frequency of the structure above the baseplate. As previously discussed, this is different from the motor reed frequency that is always a higher value than the structure reed frequency.
- Other relevant modes of vibration corresponding natural frequencies and excitation sources that may be experienced are not included within the scope of this series. Only rotating imbalance is considered.
- Should the height of the top motor bearing from the foundation be a consideration for a vibration acceptance criterion at that bearing?
- How does rigidity of the structure factor in?
- What is the effect of motor balance grade?
- How does the foundation rigidity impact vibration?
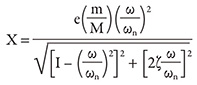 Where:
X = Amplitude of displacement of the structure at the motor CG (inches); this is the peak displacement and is doubled to obtain a peak-to-peak value.
e = Eccentricity of the rotating mass related to the residual imbalance (inches) and operating speed. This is determined by the balance grade of the motor. Refer to ANSI S2.19 or ISO 1940/1.
m/M = Dimensionless ratio of the rotating motor rotor weight (m) to the motor weight (M).
ω/ωn = Dimensionless ratio of operating speed (ω, rpm) to the structure reed frequency (ωn, cycles per minute—CPM), whether determined by calculation (as discussed in the September 2012 article) or by test.
ζ = Damping factor (dimensionless); damping factors for these types of structures in pump installations have been observed to be between 0 and 0.03 (0 to 3 percent).
The dimensionless vibration response may be depicted graphically in Figure 2.
Where:
X = Amplitude of displacement of the structure at the motor CG (inches); this is the peak displacement and is doubled to obtain a peak-to-peak value.
e = Eccentricity of the rotating mass related to the residual imbalance (inches) and operating speed. This is determined by the balance grade of the motor. Refer to ANSI S2.19 or ISO 1940/1.
m/M = Dimensionless ratio of the rotating motor rotor weight (m) to the motor weight (M).
ω/ωn = Dimensionless ratio of operating speed (ω, rpm) to the structure reed frequency (ωn, cycles per minute—CPM), whether determined by calculation (as discussed in the September 2012 article) or by test.
ζ = Damping factor (dimensionless); damping factors for these types of structures in pump installations have been observed to be between 0 and 0.03 (0 to 3 percent).
The dimensionless vibration response may be depicted graphically in Figure 2.
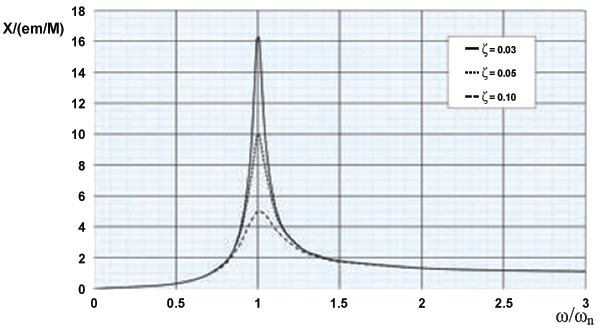 Figure 2. Vibration response for rotating imbalance
Figure 2. Vibration response for rotating imbalanceBalance Grade Decoded
For the purpose of this article, an explanation of America National Standards Institute (ANSI) and International Organization for Standardization (ISO) standard balance grades is necessary. Motor manufacturers’ standard balance grades correspond to a balance grade from ANSI S2.19 or ISO 1940/1, such as G2.5, G6.3 or some interim grade (G, millimeters/second). From ANSI S2.19 or ISO 1940/1, the grade number G refers to a value of constant velocity in units of millimeters/second. For example, G6.3 refers to 6.3 millimeters/second residual imbalance. Graphs in ANSI S2.19 and ISO 1940/1 also provide eccentricity (e, millimeters) based on the balance grade chosen and applicable operating speed. These graphs provide eccentricity values that correspond to the relationships in Equation 4. Balance grade “G” number = (e) Equation 4: [(2Π) (rpm) / (60)] Rearranging and converting the units of e to English customary units result in Equation 5, with G in millimeters/second and e in inches. e = [(60) (balance grade “G” number)] / [(2Π) (rpm) (25.4)] OR Equation 5: e = [(0.376) (balance grade “G” number)] / (rpm)Sample Studies
The input parameters required to produce resultant values of top-of-motor vibration are:- (m/M), mass ratio
- balance grade “G”
- rpm
- ζ, damping factor
- (ω/ωn), frequency ratio
The Results
- From Equation 1 and Figure 2, the vibration response is dominated by the frequency ratio (frequency separation margin).
- Vibration response varies linearly with the motor balance grade. This is expected from Equation 1, and the results in Tables 1 and 2 confirm this. Note that a motor balance grade of G2.5 yields values 40 percent of those achieved with balance grade G6.3.
- From Tables 1 and 2, the vibration response obtained is constant across different pump design operating speeds when units of velocity are used. This is expected because the excitation is constant velocity-based values of motor imbalance (balance grade). Usually higher speeds involve smaller pumps and slower speeds involve larger pumps. The results encompass a range of pump sizes. The topic of units of vibration useful for the purpose of standard acceptance criteria is discussed in the second part of this series.
- From Tables 1 and 2, the vibration response obtained with units of mils peak-to-peak is not constant but varies with the design operating speed. Again, the results encompass a range of pump sizes. The topic of units of vibration useful for the purpose of standard acceptance criteria is discussed in the second part of this series.
- A frequency separation margin of 10 percent (obtained in the field by test) produces a range of vibration responses at the top motor bearing that are reasonable.
 Table 1. Results from example one
Table 1. Results from example one Table 2. Results from example two
Table 2. Results from example twoImplications of the Results
- As shown in Equation 1 and Tables 1 and 2 with the structure reed frequency field characteristics fixed and assumed to be based on test, no inputs for top-of-motor bearing height, structural rigidity or foundation rigidity considerations are used to calculate the vibration response. Analysis of empirical field data to determine top-of-motor bearing vibration acceptance criteria should not consider these parameters, nor should acceptance criteria be based on these parameters.
- When the field structure reed frequency characteristics (based on test) are not known and are determined by calculation (such as in the pre-construction phase of a project), height and rigidity characteristics impact the value of the calculated structure reed frequency as discussed in the September 2012 article. The calculated reed frequency is included in Equation 1, with no subsequent consideration of structure height or structure rigidity.
- Predicting accurate structure reed frequencies in the pre-construction phase is important to achieve an acceptable frequency ratio.
- Because of the inaccuracies of the available structure reed frequency calculation methods, frequency separation ratio values higher than ±10 percent should be used to obtain actual separation ratio values in the field of ±10 percent when the structure reed frequency is calculated.
- To determine the structure reed frequency in the preconstruction stage and because the motor reed frequency dominates the structure reed frequency result, the motor reed frequency provided by the motor vendor must be accurate.
- Typically, different field vibration levels are measured in line with the axis of the piping versus perpendicular to the axis of the piping. This is because of the different field structure reed frequency characteristics relating to the different directions and corresponding different frequency ratio values (or frequency separation margins) that result in the different responses.
References
- Claxton, J. “Top-of-Motor Vibration,” Pumps and Systems, September 2012.
- ANSI/HI 9.6.8, Dynamics of Pumping Machinery, Hydraulic Institute, Parsippany, N.J., www.pumps.org.

