Lev Nelik answers a reader's question on thermodynamic sub-processes that are highly time dependent
05/28/2015
Letter from a Reader
The following comments relate to scenarios described in Parts 1 and 2 of “Can Deaerators Create Pump Trips?” (Pumps & Systems, March and April 2015), which discuss handling power plant transients. Steady flows to and from the deaerator (DA) and gradual isentropic thermodynamic changes from the high to low temperature/pressure conditions are assumed. A gradual power plant cool down period after a shutdown event may mitigate general or local flashing. From Part 1 at Point A:- DA total tank volume V = 20,000 gallons = 2,674 cubic feet (ft3).
- Tank liquid (water) volume (Vliq) = 10,000 gallons = 1,337 ft3.
- Mass of tank liquid
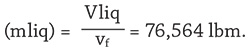
- Mass of tank vapor (mvap) = 0 lbm (all mass is saturated liquid at vf).
- Total mass of tank contents (M) = mliq + mvap = 76,564 lbm.
- Using the above values, the calculated specific volume (“v”) should agree with the temperature-specific volume (T-v) diagram at Point A. However, calculated
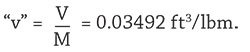
- This value is greater than vf = 0.01746 ft3/lbm from the diagram. Since the vapor volume Vvap = mvap x vg = 0 ft3, the analysis might be conducted by assuming that the total tank volume revV = Vliq + Vvap = 1,337 ft3. In other words, assume the total DA tank volume is 10,000 gallons and completely full of liquid (water) at Point A. Then, at Point A on the diagram,

Nelik’s Response
Thank you for your comments. These are very diligent and methodical calculations. I have a few notes to your comments. Your assumption of the process being gradual and isentropic cannot be assumed, because it is highly transient. This is one of the reasons it is not easy to calculate. Several thermodynamic sub-processes that are highly time dependent are taking place: convection from hotter liquid to colder, phase transformation and cooling of the vapor that is evolving back into liquid phase as it tries to rise through the colder liquid layer. Perhaps the only safe assumption for the process is that it is adiabatic, assuming no heat loss through the pipe to the surroundings occurs as a result of thick insulation. My assumption that Point A is liquid that occupies half of the tank space with zero vapor above it is problematic. While the pressure is significant, a complete absence of vapor in the space above the liquid is impossible, as it would imply full vacuum. Because the fluid in the DA is at the saturation curve or in the subcooled region, something must be present above the liquid to maintain pressure. To explain what keeps the void above the liquid at pressure in this case, we would need to understand more precisely the specifics of the DA design. Your note is well-placed; if we instead make a slight adjustment to starting Point A to be slightly into a two-phase region, this difficulty immediately disappears. The entire space above the liquid would be vapor, the combined volume in the tank could be treated as the entire tank (20,000 gallons) instead of half of it (10,000 gallons), and the total combined specific volume would be total tank volume divided by total mass (which at Point A is mostly liquid). That would make the total combined volume double that if we used only half the tank. It does not affect Point A but makes things easier when going to point B, as we now have a total volume of the entire 20,000 gallons filled with a mixture—some liquid and some vapor. From there, vapor mass fraction “x” and volume can be calculated. My assumption that the entire system is a constant volume is valid, because otherwise, it is impossible to make any other reasonable assumptions. For example, we cannot assume constant pressure at Point B (As an example, imagine that the tank had a free heavy lid that would apply constant pressure and that the expanding volume of vapor would move the lid up). The tank described in these articles does not have moveable boundaries. The only openings are to the condensate piping and through the running pumps, but those are essentially closed (by running water). As explained in Part 2, vapor wants to expand according to a new pressure to which the surface of the DA is now suddenly at (Point B). But it is not a steady state process, and things are very transient. As vapor tries to form and float up, it encounters a colder layer above it and condenses back to liquid almost instantaneously—at many orders of magnitude faster than it takes for vapor to travel through the suction header of the running (colder) pump to reach its entrance. Instead, what likely is happening is convective cooling of the hotter leg by the colder leg via this attempted vaporization and re-condensation.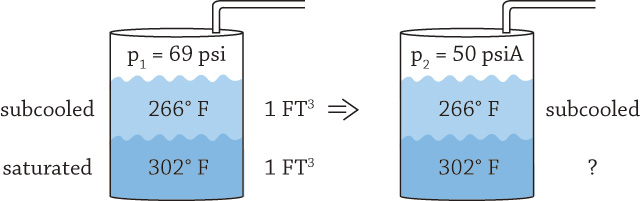 Figure 1. Visualization of vaporization and re-condensation (Courtesy of the author)
Figure 1. Visualization of vaporization and re-condensation (Courtesy of the author)
