The bolt as a screw is one of the six simple machines. A simple machine magnifies or changes the direction of an input force. By means of mechanical advantage, a bolt can dramatically increase its input force. Take for example an 8-bolt flange with 3/4-inch diameter bolts. By manual effort alone, a person can easily develop a total bolt load of over 110 tons. This article explains the mechanics by which the mechanical advantage is possible and then draws attention to how friction can deteriorate the end effect of a bolt’s mechanical advantage. The means by which a bolt can greatly magnify input load is by leverage. One source of this leverage is afforded by the geometry of the bolt. The other is the leverage from a tightening tool—in this example, a torque wrench. To illustrate the mechanics of a screw thread, consider a 3/4-inch diameter, Unified Course (UNC), A193 B7 bolt with a yield strength of 105,000 pounds per square inch (psi). Image 2 identifies the geometrical characteristics of a bolt that create leverage.
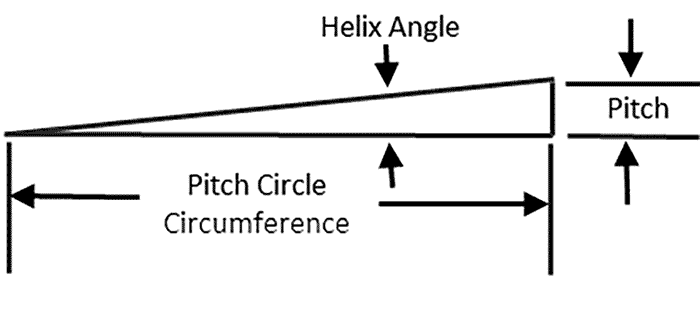 Image 1. The threads of a bolt essentially form an inclined plane (Images courtesy of Inertech, Inc.)
Image 1. The threads of a bolt essentially form an inclined plane (Images courtesy of Inertech, Inc.)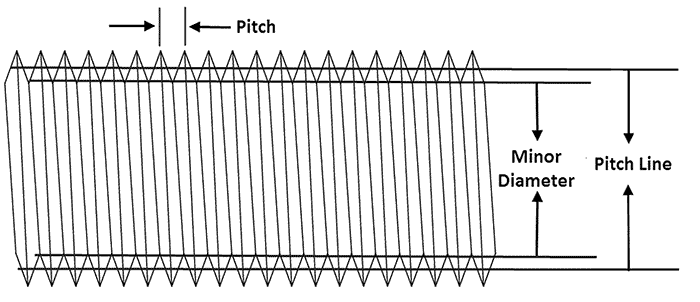 Image 2. The geometrical characteristics of a bolt that creates leverage
Image 2. The geometrical characteristics of a bolt that creates leverageT = [(pt/2 π) + (utdt/2 cos(a)) + (un dn/2)] FB/12 Where: pt = pitch of the bolt thread = 0.10 inch dt = mean contact diameter of thread = 0.685 inch dn = mean contact diameter on nut spot face = 0.8738 inch a = half thread angle = 30 degrees ut = friction coefficient on threads = 0.13 un = friction coefficient on bearing surface (spot face) = 0.08 FB = value of (single) bolt load = 17,561 lbf. T = torque, in. lbf. Equation 1
Specifically, the second term is the energy lost to friction between mating threads, while the third term accounts for the energy lost to bearing surfaces during the tightening process. Now evaluate these terms for the example bolt. In addition to bolting geometry values, consider the published values of friction coefficients for a commonly used paste, lubricant. The definition and values for each variable are noted in Equation 1. Substituting these into the respective terms they are evaluated and compared in Image 3. Term 1 is the useful work in creating the clamping force.
 Image 3. Input energy going into stretching the bolt (Term 1), and energy lost to friction (Terms 2 and 3)
Image 3. Input energy going into stretching the bolt (Term 1), and energy lost to friction (Terms 2 and 3) 
