First of Two Parts
02/11/2016
Using the example system in Figure 1, this series will focus on the process elements found in piping systems. In this example, a process fluid is pumped from a storage tank, PX-TK-120, through an end suction pump, PX-PU-120, specified to pass 800 gallons per minute (gpm) with 202 feet of head. From the pump discharge, the 80 F process fluid travels to a heat exchanger, PX-HX-121, where the fluid is heated to 120 F. Level control PX-LCV-120 maintains the level in process vessel PX-PV-122 to 15 feet. The system boundaries are the tanks PX-TK-120 and PX-VP-122. The system contains only one circuit. Table 1 lists the physical properties of the process fluid.
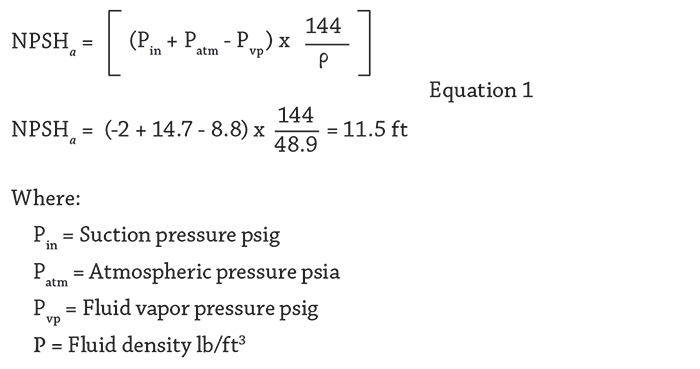
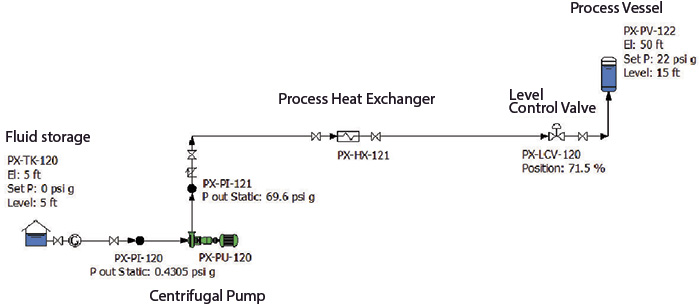 Figure 1. Example system consisting of the items making up the system along with displayed operating data (Graphics courtesy of the author)
Figure 1. Example system consisting of the items making up the system along with displayed operating data (Graphics courtesy of the author) Table 1. Physical properties of the process fluid used in this example
Table 1. Physical properties of the process fluid used in this example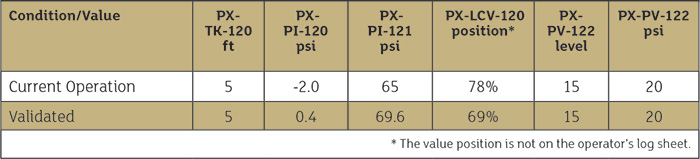 Table 2. Comparing as observed conditions with cavitation to validated results
Table 2. Comparing as observed conditions with cavitation to validated results
