Pump System Improvement
06/06/2016
Editor’s note: This article provides additional information that further explains Ray Hardee’s monthly Pump System Improvement column appearing in the June 2016 issue. Read it here.
The various calculations used in the power cost balance sheets in June’s Pump System Improvement column, which were shown in Tables 1 and 2 on page 22 of the June issue of Pumps & Systems (see them below), are documented in industry standards, along with methods covered in fluid dynamics texts. This article will demonstrate these calculations and provide additional details that explain how the conclusions were derived.
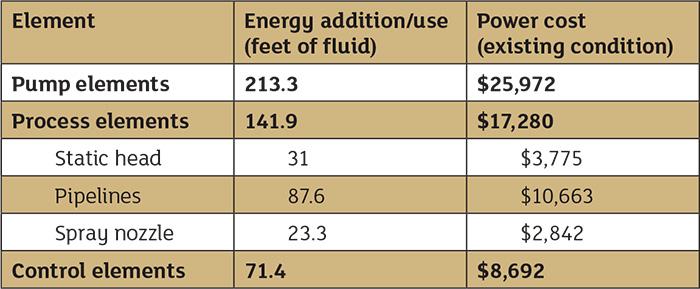 Table 1. Power cost balance sheet for the spray system prior to system improvements
Table 1. Power cost balance sheet for the spray system prior to system improvements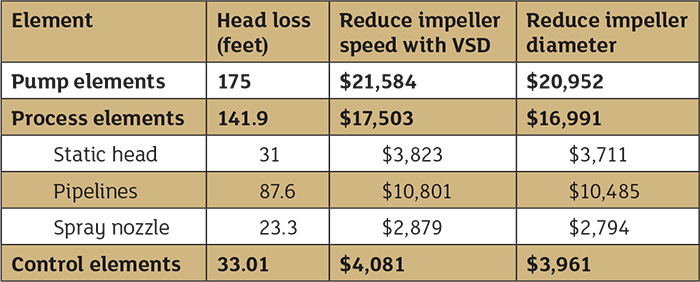 Table 2. Comparison costs of reducing impeller speed by incorporating a VSD and reducing impeller diameter
Table 2. Comparison costs of reducing impeller speed by incorporating a VSD and reducing impeller diameterCalculating the Pump Elements
The manufacturer’s supplied pump curve is the primary document for pump operation. A curve for the spray pump is shown here as Figure 2.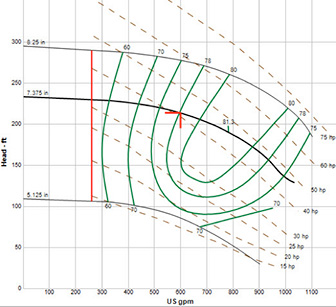 Figure 2. The pump curve for the spray pump operating at 3,550 rpm provides the necessary pump performance data for energy and power calculations. (Graphics provided by the author)
Figure 2. The pump curve for the spray pump operating at 3,550 rpm provides the necessary pump performance data for energy and power calculations. (Graphics provided by the author)
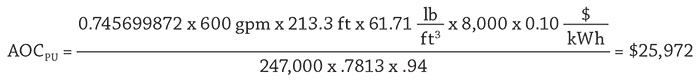
Calculating the Process Elements
Next, we will look at the process elements using energy to provide the static head across the system; overcome the head loss of the process fluid passing through the pipe, valves and fittings; and provide the differential pressure across the spray nozzle to achieve the proper fluid distribution. All of the system energy is provided by the pump, so if we can determine the head loss across these devices along with the flow rate through them, we can determine the amount of power provided by the pump that is used for each process element item. We will first look at the energy and power required for the fluid to overcome differences in elevation and pressure across the system.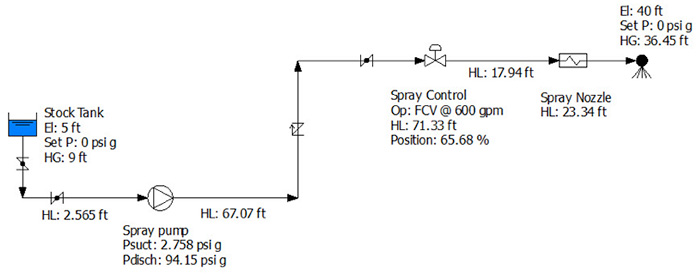 Figure 3. The design data and calculated results needed to perform all head loss and power calculations for the process and control elements
Figure 3. The design data and calculated results needed to perform all head loss and power calculations for the process and control elements
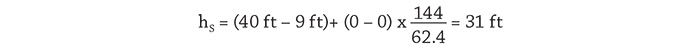

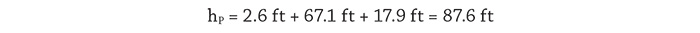

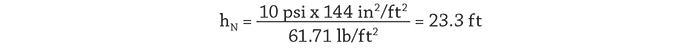
Cost of the Control Valve
The International Society of Automation (ISA) has developed standard ISA-75.01 Flow Equations for Sizing Control Valves, which is used by control valve suppliers for the selection of control valves. The standard consists of a number of equations documenting the process. Control valve selection is outside the scope of this article, but the formulas presented within the standard can be used to determine how a given control valve will operate in the system. From the plant operating data we know that the flow rate through the spray control valve is 600 gpm, and from the valves stem indicator we can determine the valve position. Using the manufacturer’s supplied control valve data, we can determine the valves Cv, or flow coefficient, for a given valve position. Using the flow coefficient Cv in the valve sizing equations, the differential pressure across the control valve can be calculated. Equation 4 shows the valve sizing equation rearranged to determine the differential pressure.
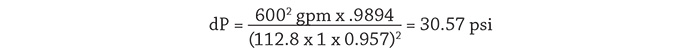
Considering the Options
With the power cost balance sheet, we know the pumping cost in operating the system, along with the cost of each item with the system. With this information, we can look for ways to reduce the total cost. In this system, with 71.4 feet of head loss across the control valve and an annual control valve operating cost of $8,696, everyone involved with the system has an estimate on the savings potential. After discussions with the control valve supplier, we found the spray control will work properly with only a 10 psi pressure drop. Plant staff decided on a 15 psi pressure drop to provide additional operating margin. The control valve equipment supplier was consulted prior to making any plant recommendation. Further, the valve supplier stated that the cavitation occurring within the control valve would be eliminated with a lower differential pressure across the valve. The pump supplier was asked for ways to reduce differential pressure across the pump by 15 psi. The supplier returned two options: installing a variable speed drive (VSD) to reduce the pump head or reducing the impeller diameter to develop less head. Saving on operating costs is just one consideration in system improvements, but it helps everyone grasp the magnitude of the possible savings. As a result, a power cost balance sheet was developed for both the VSD option and reducing impeller diameter for system improvement. For each option, we must use the manufacturer’s supplied pump data to arrive at the annual operating cost for the pump elements. Table 3 provides the needed data from the pump curves for each option. Looking at the variable speed option, installing a VSD reduced the pumping cost to $21,584, while trimming the existing pump impeller results in a pumping cost of $20,952.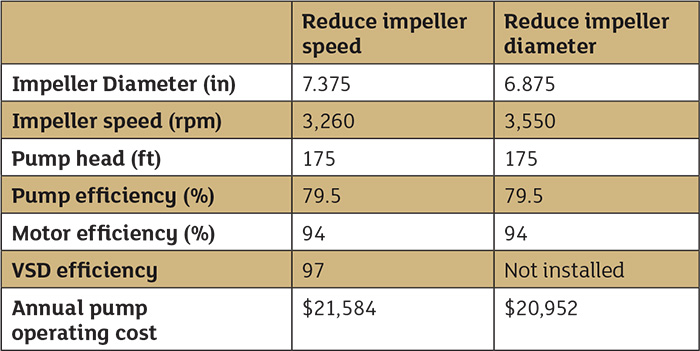 Table 3. The pump performance data for the spray pump with a flow rate of 600 gpm, pumping a fluid with a fluid density of 61.71 lb/ft3
Table 3. The pump performance data for the spray pump with a flow rate of 600 gpm, pumping a fluid with a fluid density of 61.71 lb/ft3Wrapping Things Up
The power cost balance sheet provides detailed cost information for operating existing pumped systems. It provides everyone involved with the project a way to identify the system’s high-cost items and look for ways to make improvements. The real benefit of the power cost balance sheet is that it allows each improvement option to be calculated and compared with other available options. As shown in this example, a large number of calculations are required to develop this cost data. But with the availability of piping system simulation software and electronic spreadsheets, these tedious calculations can be automated to provide a clear picture of existing costs, along with an accurate estimate on potential cost savings.
See more Pump System Improvement articles by Ray Hardee here.

