Imagine watering flowers in your yard. When your thumb is halfway over the opening of the hose, the water sprays out 10 feet or so onto your petunias. But when you move your thumb three-fourths of the way over the opening, does the water spray out a longer or shorter distance, and does more or less water come out of the hose? Of course, the water goes a longer distance, and less water comes out of the hose. The reverse is true when you cover less of the hose opening. If you understand this very simple concept then you also understand how 99 percent of centrifugal pumps work. A centrifugal pump uses a rotating impeller to convert input power (usually from a motor) into kinetic energy. Fluid enters the eye of the impeller and is transferred radially into, in most cases, an expanding volute. There is a conversion of velocity energy to pressure energy in the volute, and voila, pressure is generated and the fluid goes out of the pump and into the downstream piping. Centrifugal pumps can deliver high or low flows at low or high pressures, all depending on the application and what specific pump is applied.
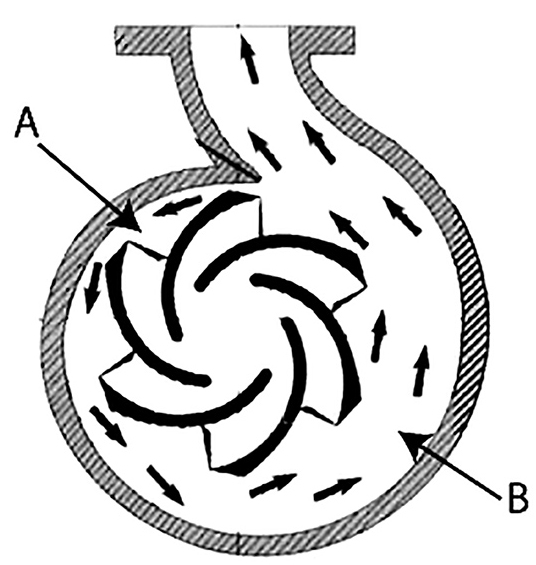 Figure 1. Pump casing (Graphics courtesy of Cummins-Wagner)
Figure 1. Pump casing (Graphics courtesy of Cummins-Wagner)Regardless of manufacturer or style, most centrifugal pumps have several common parts: impeller, casing, packing or seal, and bearings. The impeller is the component that adds energy to the fluid. Most impellers are either enclosed, which means that they have a front shroud covering the vanes of the impeller, or open, meaning no front shroud. The casing is manufactured with either flanged or threaded connections. The casing transfers the liquid from the impeller through the volute to discharge. Most pumps use an expanding volute with a casing cutwater. At point A, the area within the volute is smallest, the velocity is highest and the pressure is lowest (see Figure 1). As the fluid travels through into the expanded area B, the area within the volute increases, the velocity decreases and the pressure increases. This is the velocity energy to pressure energy conversation. The packing or mechanical seal is used to seal the pump and prevent fluid from leaking into the environment. The bearing housing is mounted to the back of the casing and carries the bearings that are mounted on the pump shaft, used to absorb radial and axial thrusts generated by the pump.
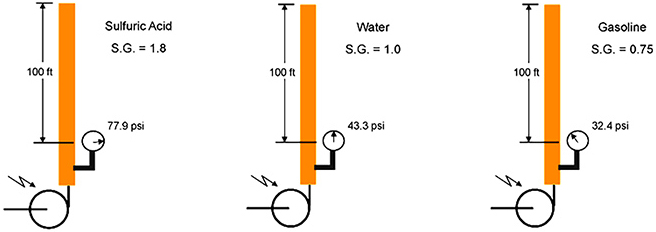 Figure 2. TDH example
Figure 2. TDH exampleThe Pump Curve
Ninety nine percent of centrifugal pump curves look similar, which also means that 99 percent of centrifugal pumps operate the same way. Flow, usually expressed in gallons per minute (gpm) is on the X-axis and pressure, expressed in total dynamic head (TDH) is on the Y-axis (see Figure 3). TDH is used instead of pounds per square inch (psi) because any given centrifugal pump will produce the same TDH, expressed in feet of liquid pumped, irrespective of specific gravity (SG). The calculation for TDH is: (PSI x 2.31)/SG). 2.31 is the constant for 1 pound of pressure being developed by a 2.31 foot high column of water.
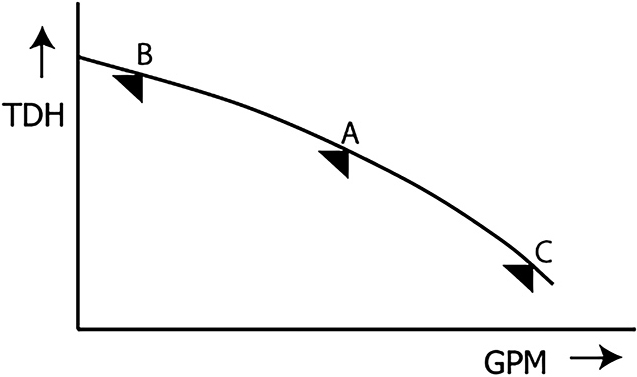 Figure 3. Pump curve
Figure 3. Pump curveFigure 2 shows that pumping water at 43.3 psi produces 100 TDH (think of a column of water 100 feet in the air). Even though the pressure gauge on the sulfuric acid application shows a much higher pressure, the resultant TDH is still 100 feet. The reverse it also true for the gasoline application; lower pressure but the same 100 TDH. The formula provided above is probably the most important formula for the pump application engineer to know, especially when troubleshooting running pumps. In many cases, all you have in the field is a pressure gauge and a pump speed. Converting the pressure to TDH allows you to begin to plot points on a curve, “backing into” gpm, helping to understand where the pump is running on the curve. It is important to note that TDH is total dynamic, or developed, head. This takes into account only the actual work the pump does. So when calculating head, the suction pressure must be subtracted from the discharge pressure before the conversion to TDH. Also remember the horsepower required to do the same amount of work. It requires more horsepower to pump a heavier fluid the same distance. Now, back to the pump curve. Centrifugal pumps are dynamic machines, or as I like to say it, they are dumb. They are slaves to the system that they are installed in. The centrifugal pump represented by this curve can run anywhere on the curve. Let’s go back to the garden watering example. So, we’re back to your thumb being half over the hose. You are “pumping” a certain flow, let’s call it 10 gpm at a TDH of 15 feet. The pump is running at point A on the curve (see Figure 3). You then put your finger three-fourths over the hose opening; less flow, more pressure. Now the pump is running at point B on the curve. Now you move your finger to cover only one-fourth of the opening; more flow, less pressure. Now the pump is running at point C on the curve. Now change the hose to discharge piping, and change your finger to a discharge control valve. When you close down on the valve, the pump moves to the left and up. When you open the valve, the pump moves to the right and down. The pump is dumb. It only will run on that curve where the system allows it to. It does not care what you thought you designed the pump for, or what you thought you specified the conditions to be. It will only run where the system allows it to run. It is not uncommon to get the following call from an end user: “I specified 150 gpm at 80 TDH. We’re only getting 80 gpm from the pump, something must be wrong with the pump.” We actually hope that something is wrong with the pump because those problems are the easiest to solve. But my “gut” estimate from 28 years of experience is that 95 percent of these issues have nothing to do with the actual pump. Maybe there was a 100-foot stretch of pipe the user thought was 4 inches in diameter but is actually only 2 inches. Maybe there was a filter installed somewhere in the system that the end user was unaware of. In either case, the pump is likely running where the system is allowing it to run. So we’ve reviewed the basics of pump curve: flow, head and general operation. Let’s look at some other important aspects of centrifugal pumps.
Brake Horsepower (BHP)
Brake horsepower (BHP) represents the rate at which energy is added to the fluid. It is calculated by (TDH x gpm x SG)/ (3960 x pump %). Let’s use the example of 175 gpm at a TDH of 70. The SG of the fluid being pumped is 0.95 and the efficiency from the manufacturer’s pump curve is 68 percent.

Efficiency
Every pump exhibits internal losses while pumping. The amount of loss depends largely on the size and design of the pump, as well as where the pump is operated on its performance curve. Each pump is designed for a specific flow and pressure (TDH) at a specific rpm. When the flow deviates from the design flow, the liquid does not enter the vanes at the correct angle, and extra turbulence and hydraulic losses occur. Losses are lowest and efficiency is highest at the best efficiency point (BEP). This is also where the pump is most hydraulically and mechanically stable.
.jpg) Figure 4. Pump performance curve
Figure 4. Pump performance curveFigure 4 shows a typical pump performance curve. You will notice that its general shape is very similar to the simple, one-line curve that we showed initially. The pump impeller can be trimmed to a minimum diameter of 7 inches and has a maximum diameter of 10 inches. Theoretically, there can be an infinite number of impeller diameters supplied; however, most manufacturers trim in 1/8-inch increments. With the impeller diameter selected, the pump can now run anywhere on that impeller diameter curve, but only on that impeller diameter curve, assuming constant speed. The parabola-shaped lines are the efficiency lines. So, with a 10-inch diameter impeller, the maximum efficiency for this pump is 70 percent while the minimum shown efficiency is 55 percent. However, once the impeller is trimmed, the BEP changes. The BEP using an 8-inch impeller is approximately 67 percent, in-between the 65 percent and 68 percent efficiency lines but closer to the latter, hence 67 percent. The corresponding gpm and TDH would be 155 and 55 respectively.
.jpg) Figure 5. Pump 1, 3 x 1.5-6
Figure 5. Pump 1, 3 x 1.5-6The straight, dashed lines running from upper left to lower right on the curve are the BHP lines. Using our earlier example of 175 gpm at 70 TDH, you can estimate the BHP by plotting the point on the curve. The point is in-between the 3 hp and 5 hp lines but closer to the 5 hp, so a reasonable estimate would be 4 to 4.5 BHP. Our calculation above revealed 4.3, proving that a good estimate can be visually obtained from the curve, assuming that SG is close to 1.0. All users want to run the most efficient pump(s) possible. That said, in this author’s opinion, what is more important is where the pump is operating on the performance curve. The best way to illustrate this is the simple example below. Let’s pick an arbitrary rating of 200 Gpm at 130 TDH. Both pumps in Figures 5 and 6 can do this rating. Pump 1 is at BEP and has an efficiency of 70 percent. Pump 2 is running to the left of the curve but has an efficiency of 74 percent. Which pump do you select? That’s an easy one.
.jpg) Figure 6. Pump 2, 3 x 206
Figure 6. Pump 2, 3 x 206The 74 percent efficient pump, right? After all, it’s more efficient. Well, I’d pick the first pump and sacrifice the four percentage points in efficiency. Why? Because that pump is running at its hydraulically and mechanically most stable point on the curve. That is not to say that the 3x2-6 is running at a terrible point on the curve. And, regarding efficiency, and assuming a water application, the BHP difference is only 0.5 (9.4 BHP vs. 8.9 BHP). I am not understating the importance of energy conservation in the 21st century; however, I will gladly sacrifice 0.5 BHP for a more reliable, stable operating pump. With larger flow applications this may not be as straightforward. At 16,000 gpm at 240 TDH, the difference between 86 and 83 percent efficiency is over 40 hp. Imagine plugging in a 40 hp motor and letting it run 24/7 over in the corner of your facility for the next 25 years. So, my point here is, efficiency is not the be-all and end-all. It is one consideration when selecting a pump.

