Pumping Prescriptions
Pumping Machinery LLC
10/16/2017
Seal failures are the number one headache for many operators when it comes to pump reliability concerns. However, these failures are usually indicators of an underlying issue. Seal failure is rarely caused by a problem with the seal’s design or a fault during seal or bearing production. The primary reasons seals fail are:
- improper operating flow (significantly off the best efficiency point [BEP])
- absence of (or poor) seal flush for dirty liquids
- poor alignment (driver to pump, or piping to pump)
 For a circular shaft I = 3.14 x D4/64, and thus a deflection at a given force is proportional to:
y ~ L3/D4, or abbreviated it is often written as L3D4
For a circular shaft I = 3.14 x D4/64, and thus a deflection at a given force is proportional to:
y ~ L3/D4, or abbreviated it is often written as L3D4
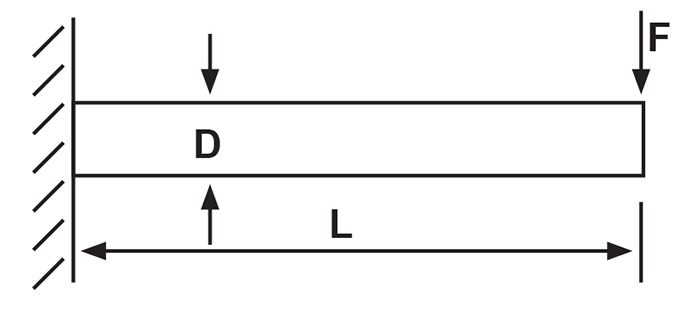 Figure 1. The pump shaft deflects under load, as a structural beam. (Graphics courtesy of the author)
Figure 1. The pump shaft deflects under load, as a structural beam. (Graphics courtesy of the author)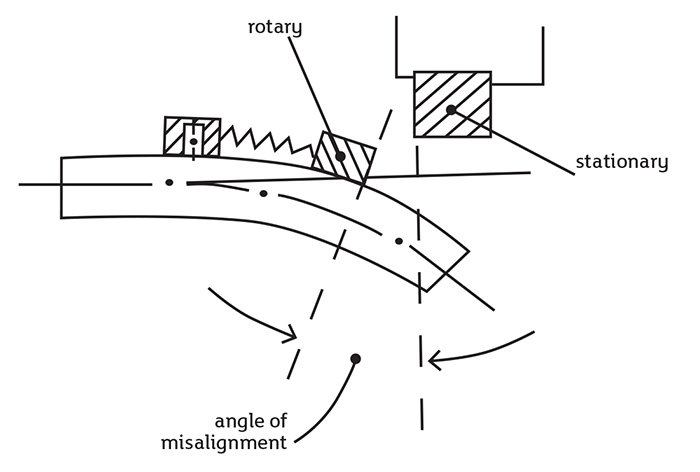 Figure 2. Seals will leak as excessive loads cause shaft deflection and seal face misalignment.
Figure 2. Seals will leak as excessive loads cause shaft deflection and seal face misalignment.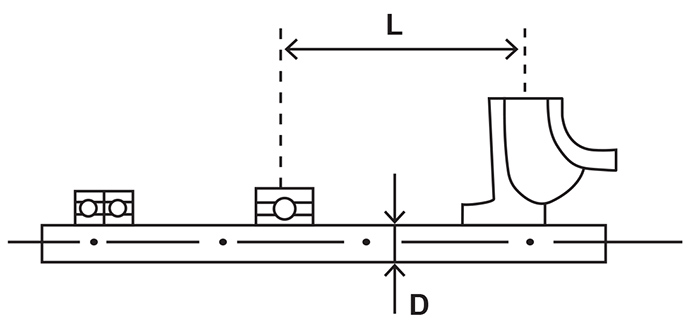 Figure 3. L and D parameters for a pump rotor.
Figure 3. L and D parameters for a pump rotor.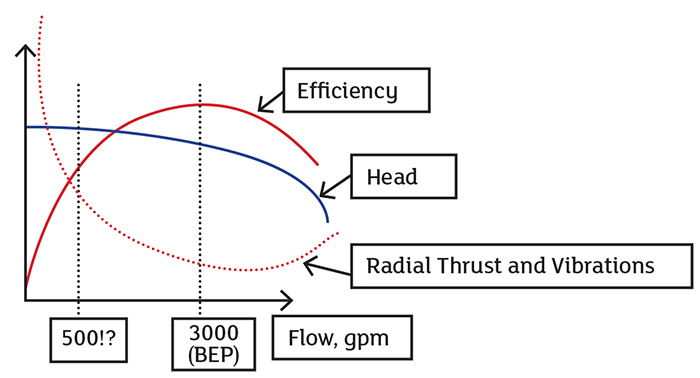 Figure 4. It is the high hydraulic radial thrust—and not the weight of the impeller—that causes excessive deflection and seal failures.
Figure 4. It is the high hydraulic radial thrust—and not the weight of the impeller—that causes excessive deflection and seal failures.Question for Dr. Pump
Mike Wisnoski Reliability Engineer, John Crane Upon reading a recent article I had a few questions regarding the “Pressure (Head) Method.” Isn’t this method only valid for pumps with suction/discharge sizes that are equal? eg 3x3 or 4x4, etc. Thus, is one better served to find flow for a said pump in the field by using the following method:- Measure differential pressure at the pump. Convert to head etc.
- Pull pump curve and look at performance line for pump with impeller installed.
- Determine the velocity head for several points on performance curve line.
- Subtract total head shown on pump curve from velocity head from a.
- Replot head vs. flow using this new head. (Basically static head + elevation)
- Use this curve as compared with field measurements as this is what is measured in the field using gauges. (Unless pitot tube is used)
To read more Pumping Prescriptions columns, click here.

