The Eighth in a Series
Normalizing NPSH
Our attempts to normalize or classify water turbine hydraulic performance culminated in 1915 with the development of the specific speed concept, which was later applied to centrifugal pumps (2).
Because NPSH is not included in specific speed, however, attempts continued to understand and normalize this elusive characteristic. In 1922 (1), the Thoma‑Moody parameter, Sigma, was introduced and defined as:
Sigma = σ = NPSH/H (13‑1)
where H is the total head of the first stage impeller. Sigma was widely accepted and used for a number of years, but it had a significant shortcoming, since the NPSHR of a pump is relatively independent of the head produced by the pump.
In 1937, three engineers at Worthington-Karassik, Wislicenus and Watson-were assigned the task of developing a better concept than Sigma. Initially working independently, they joined forces. While discussing their problem over Saturday morning coffee in Karassik's kitchen, they developed the concept of Suction Specific Speed (3).
Definition of Suction Specific Speed
Suction specific speed, like specific speed, is not a speed at all. It is an index number, or "yardstick." It is based on the NPSHR of a centrifugal pump, normally the 3 percent head drop NPSHR and normally at its best efficiency point (BEP). The equation for suction specific speed is the same as specific speed, except that NPSHR is substituted for head, as follows:
S = ![]() (13-2)
(13-2)
Where (in U.S. units):
S = Suction Specific Speed
N = RPM of Pump
Q = Pump Capacity*†, GPM
NPSHR = NPSH required by pump†, feet
*If the impeller is double suction, Q in the above equation is one-half the BEP capacity of the pump. This is a major difference from calculating specific speed, in which we use total pump capacity, whether the impeller is single suction or double suction.
†Normally calculated at the BEP
The symbol Nss is often used in place of S for suction specific speed.
The value of S for most pumps is typically between 7,000 and 15,000. The higher values are more common in higher speed, higher capacity units. (See next month's article for additional discussion of the effect of speed and capacity on S.)
Problem No. 1: Suction Specific Speed
Calculate the suction specific speed for the pump represented by the performance curve in Figure A (Figure 2 from the May column).
N = 3,550 rpm
Qbep = 450 gpm
NPSHRbep = 14 ft
S =![]() =
=![]() =10,400 (RPM-GPM-FT)10,400 (RPM‑GPM‑FT)
=10,400 (RPM-GPM-FT)10,400 (RPM‑GPM‑FT)
(Our answer is different than the 9,000 stated on the curve.)
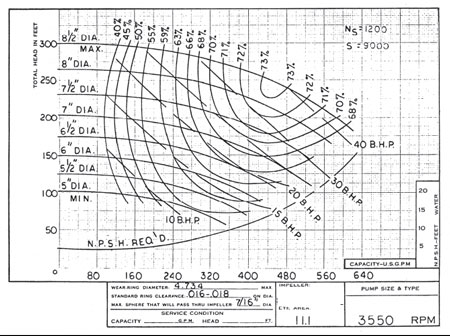
Figure A. Typical published performance curve. Single-line NPSH curve.
Importance of Suction Specific Speed
Establishing a Maximum Value for S
For a number of years, the push from users and competitors required pump manufacturers to continually strive for lower values of NPSHR. The philosophy was that "The lower the NPSHR, the better the pump." (NPSHR in centrifugal pumps is normally reduced by increasing the diameter of the impeller eye, as shown in Figure 1.) That philosophy has now changed. Due to problems that have been attributed to oversized impeller eyes, pump users have established maximum values for S, which establishes minimum values for NPSHR.
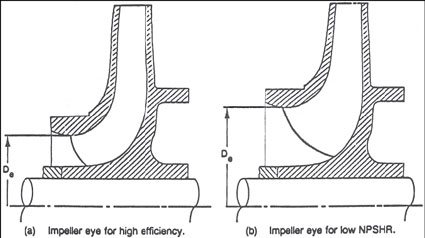
Figure 1. To reduce NPSHR, the impeller eye diameter is increased.
Establishing a "Stable" Window of Operation
Every centrifugal pump would like to run at its BEP-always. All pump components would experience maximum life at that capacity.
Seldom does a pump run at its BEP, but component life will be significantly extended if it operates within its "stable" window of capacities.
To a large extent, suction specific speed indicates the size of that window. Pumps with lower values of S have larger windows.
Suction Recirculation, or the "Big Eye Syndrome" (Monster or Myth?)
For decades, industry recognized that centrifugal compressors would "surge" if operated below a certain capacity, but only more recently have we recognized that centrifugal pumps have a comparable characteristic.
We now know that any centrifugal pump will experience recirculation in the impeller eye if the capacity is below a certain value. Larger impeller eyes and higher speeds (i.e., higher peripheral velocity of the eye-U1) produce higher energy recirculation.
The large eye required to obtain low NPSHR leads to the problem of (higher energy) "eye recirculation" or "suction recirculation" (4). As shown in Figure 2, flow through the eye is proper at the BEP, but at some reduced capacity, recirculation starts in the large eye. As pump capacity is further reduced, the intensity of the circulation increases, sometimes resulting in a reversal of flow at the i.d. of the suction pipe, near the pump. If strong enough, this vortex causes cavitation, noise and pulsations. The capacity, at which this recirculation starts, increases as the eye diameter is increased.
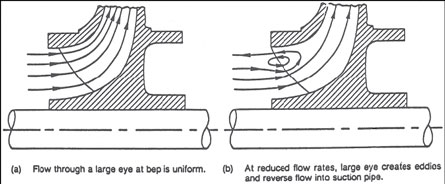
Figure 2. Although resulting in reduced NPHR at the BEP, the large eye creates eddies and recirculation at reduced flow rates.
When the vortices are strong enough to cause cavitation, the vapor bubbles collapse on the driving side, or pressure side, of the impeller vane, near the eye. If the vane twists as it enters the eye from the larger diameter, this part of the vane cannot be seen by looking directly into the eye, but must be viewed with the assistance of a small mirror.
Study by Hallam
Numerous technical papers and articles reported problems caused by suction recirculation, but none quantified the phenomenon until Hallam (5) reported in 1982 the results of a 5 year study of 480 centrifugal pumps in Amoco's Texas City refinery. Most of these pumps were in hydrocarbon services. The remainder pumped water. The average power requirement was about 150 hp and the maximum was 1,000 hp.
Figure 3 shows the results of the study. The pumps were divided in groups according to their suction specific speed. The average numbers of failures/year/pump were plotted for each group. A failure was defined as any problem with the pump that required service in the refinery repair shop. The graph shows an increase in failure frequency of almost 100 percent above an S of about 11,000.
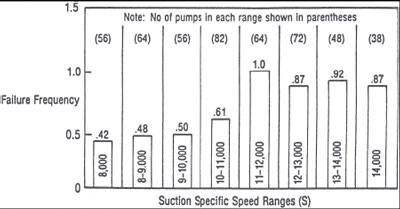
Figure 3. Failure frequency vs. suction specific speed (J.L. Hallam, [5])
The logic contained in some of the papers on suction recirculation is not totally rigorous. Most of the symptoms attributed to recirculation can be attributed to other centrifugal pump phenomena. The high S attributed to some centrifugal pumps has also been found to have been obtained by improper methods of NPSH testing. Ross (6) claims that the problem of suction recirculation has been distorted-that it simply boils down to inadequate NPSHA.
Regardless of the reason for the problem-whether it is suction recirculation, improper methods of testing or just inadequate NPSHA-Hallam's paper clearly shows that a pump with a suction specific speed greater than 11,000 should be selected with caution.
This finding caused a number of companies to prohibit the purchase of a pump with a suction specific speed in excess of 11,000.
Problem No. 2. Suction Specific Speed for a High Speed Multistage Waterflood Pump
A four-stage pump is operating on an offshore platform in waterflooding (secondary recovery) service. Figure 4 is a redrawn copy of the performance curve provided by the pump manufacturer. The pump is equipped with a double suction, first stage impeller.
Calculate the suction specific speed:
S =![]() =
=![]() = 12,000 (RPM-GPM-FT)
= 12,000 (RPM-GPM-FT)
Would you suspect that this pump could be a problem? Yes, and it was. The first stage impeller would periodically experience cavitation-erosion on the pressure side of the vanes, throwing the rotor out of balance and causing excessive vibration.
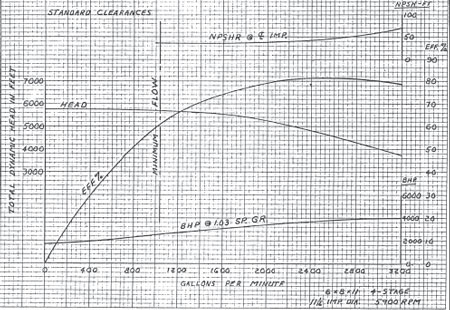
Figure 4. The vendor performance curve for the waterflood pump
Pumps & Systems, September 2009
Terry Henshaw is a retired consulting engineer who designs pumps and related high pressure equipment and conducts pump seminars. For 30 years, he was employed by Ingersoll Rand and Union Pump. Henshaw served in various positions in the Hydraulic Institute, ANSI Subcommittee B73.2, API 674 manufacturers' subcommittee and ASME Performance Test Code Committee PTC 7.2. He authored a book on reciprocating pumps, several magazine articles and the two pump sections in Marks' Handbook (11th Edition). He has been awarded six patents. Henshaw is a registered professional engineer in Texas and Michigan, is a life fellow of the ASME and holds engineering degrees from Rice University and the University of Houston. He can be reached by e-mail at pumprof@att.net.
References
Graber, P., "Solids Handling Pumps-Part 2", World Pumps Magazine, 1983
Stapanoff, A. J., Centrifugal and Axial Flow Pumps, John Wiley & Sons. Inc., 1948
Karassik, Igor J., "NPSH Characteristics of Centrifugal Pumps," paper presented at the Pump Workshop of the Pacific Energy Association, Long Beach, CA, Jan. 1981.
Shepherd, W.O. & Godin, R. L, "Face Up to Feedpump Cavitation", Power, May 1977.
Hallam, J. L., "Centrifugal Pumps: Which Suction Specific Speeds are Acceptable?", Hydrocarbon Processing, April 1982.
Ross, Robert R., "Theoretical Prediction of NPSHR for Cavitation Free Operation of Centrifugal Pumps", United Centrifugal Pumps, about 1982.

