Suction Specific Speed (Part Two)

Graph of Minimum Continuous Flows

In 1982, Richard Dubner of Chevron developed a graph for use in establishing minimum continuous flow rates for centrifugal pumps (see Figure 1). It allows a lower flow rate for pumps handling hydrocarbons than for those pumping water, and it requires larger pumps to operate closer to the BEP than smaller pumps.

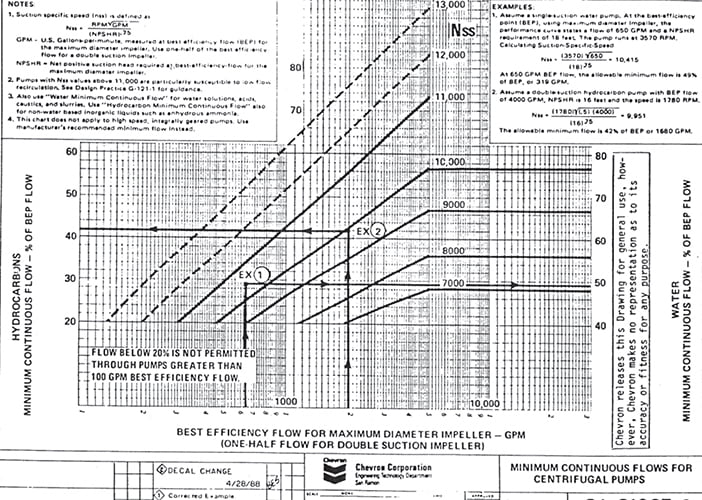
Figure 1. Dubner's (Chevron) Chart for Minimum Capacity

Note that Figure 1 cautions against S values greater than 11,000, and prohibits operation of any pump larger than 100 gpm (BEP) from operating continuously at less than 20 percent of BEP.

This graph may be used to establish operating guidelines for existing pumps, and in the selection process for new pumps to eliminate offerings that have a minimum flow above that anticipated for the intended service.

Problem No. 1. Minimum Continuous Capacity Using Dubner's graph (Figure 1), determine the recommended minimum continuous capacity for the pump in Problem No. 2 ). Qeye = 1,250 gpm S = 12,000 Pumpage is water. From Dubner's graph, we read a factor of 0.76. Qmincont = (0.76)(2450) = 1,860 gpm

"Stable" Window of Operation

In 1985, Lobanoff and Ross (1) provided the graph shown in Figure 2. It provides not only a minimum capacity, but also a maximum capacity for "stable" pump operation. It represents test results of a 4 in (discharge) pump with eight different impellers. The onset of instability was determined by measuring pump vibration. The minimum flow values obtained from this graph compare favorably with Dubner's water values (Figure 1).

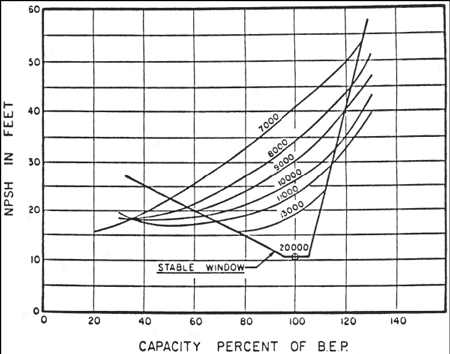
Figure 2. "Stable" Flow Range vs. Suction Specific Speed for a 4 in Pump

Figure 3 is an adaptation of the Lobanoff‑Ross graph. Dick Allen developed the graph in 1990 to assist in evaluating pump bids. It provides a method for evaluating the size of the stable window by penalizing pumps that have smaller stable windows (higher suction specific speeds).

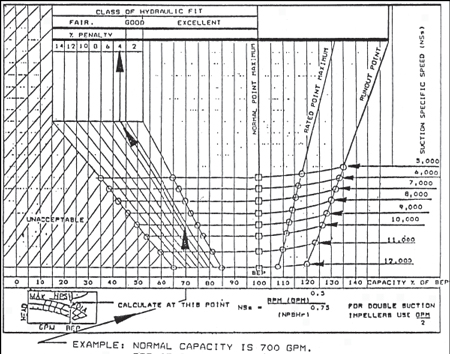
Figure 3. Centrifugal Pump Stable Window of Operation Based on Suction Specific Speed (Courtesy Dick Allen)

The penalty values are arbitrary, based on the judgment of the graph's author, and may be revised to suit the experience and philosophy of a given company.

Key points made by this graph:

1.    Do not buy a pump to operate continuously at a capacity within the "unacceptable" area (roughly any capacity less than 50 percent of Q_bep).

2.     To operate in the "excellent" hydraulic range, capacity must be higher than the "penalty" range (roughly 75 percent of Q_bep).

3.     Do not buy a pump to operate continuously at a capacity higher than Q_bep.

4.     Do not buy a pump rated at a capacity higher than about 115 percent of Q_bep.

Increased Reliability

Reliability of existing pumps can be increased by maintaining flow rates within the guidelines established by Figures 1 and 2.

Reliability of future pumps can be increased by using these graphs to establish a maximum suction specific speed acceptable for the intended service.

Effect of Speed on Suction Specific Speed

Although specific speed does not change as a pump's speed is changed, suction specific speed does change. Because of the 1.5 exponent relationship between NPSHR values (Understanding NPSH, August 2009), a pump will have a higher S when it runs at a higher speed (because the NPSHR is based on the 3 percent head drop).

To establish the effect of speed on S, substitution of NPSH₂ = NPSH₁ (N₂/N₁)^1.5 into a ratio of S equations,

S = 

yields the following relationship:

S₂ = S₁ 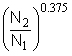                                   (13-3)

      Where:

      S₂ = Suction specific speed at second speed

      S₁= Suction specific speed at first (base) speed

      N₂ = RPM of pump at second speed

      N₁ = RPM of pump at first (base) speed

Suction specific speed, based on the 3 percent head drop criterion for the same pump, varies as speed to the 3/8^th power. (Doubling the speed increases S by 30 percent.)

Although a correction for a speed difference would seem to have value, the author is unaware of any speed adjustment now made in suction specific speed evaluations. The following is therefore offered for consideration.

Most process pumps, at least in the United States, are tested and rated at 3,550 rpm. Because NPSHR is measured at 3,550 rpm, S is calculated for that speed. To normalize all suction specific speeds to 3,550 rpm, the following equation, from Equation 13‑3, can be used:

S₃₅₅₀ = S 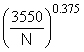                                 (13-4)

     Where:

     S₃₅₅₀ = Suction specific speed, normalized to 3,550 rpm

     S = Suction specific speed established by testing (NPSHR for a 3 percent head drop)

     N = Test speed, rpm

       Example:

       Test speed = 1,770 rpm; S = 8,500

S₃₅₅₀ = 8500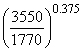= 11,000

Effect of Capacity on Suction Specific Speed

Yedidiah (2) plotted (on log‑log paper) values of S versus Q for several hundred pumps made by 10 companies, all running at 1,750 rpm. The scatter of points showed about a 2:1 variation in S for all capacities from 30 gpm to 4,000 gpm. He drew a single line though the approximate center of these points and measured the slope at about 0.18, indicating S=KQ^0.18, but stated that this exponent would be 0.125 "under ideal conditions."

Evaluating the same set of points, this author measures a slope of about 0.15, acknowledging that a slope of 0.125 would also fit the points satisfactorily.

Effect of Capacity and Speed on Suction Specific Speed

Yedidiah (2) also stated that as a function of speed, S "should" vary as S=AN^0.25.

If we let the capacity exponent be 0.125, and the speed exponent 0.25, and if we assume that these exponents apply while holding the other variable constant, we can write the following equation:

S = C Q^0.125N^0.25

Solving for C for the best fit with the second Yedidiah graph (and it fits reasonably well) results in

S_typ = 550 Q^0.125N^.25                         (13-5)

     Where (in U.S. units):

     S_typ = Suction specific speed of a "typical" pump

     Q = Pump capacity* at BEP, GPM

     N = RPM of pump

*If the impeller is double‑suction, Q in the above equation is one-half the BEP capacity of the pump.

This equation can be used to calculate S for a "typical" pump, realizing that published performance data may show a value 40 percent above or below the "typical" value.

A more useful purpose may be to further "normalize" suction specific speed. Equations 13‑3 and 13‑4 provide for normalizing S for a particular pump to a common speed, such as 3,550 rpm. Equation 13‑5 can be massaged to provide normalization of speed and capacity for different pumps, resulting in Equation 13-6:

S₂=S₁(Q₂/Q₁)^0.125(N₂/N₁)^0.25 (13-6)

     Where:

      S₂ = Suction specific speed of second pump

      S₁ = Suction specific speed of reference pump

     Q₂ = BEP capacity (per eye) of second pump

     Q₁ = BEP capacity (per eye) of reference pump

     N₂ = RPM of second pump

     N₁ = RPM of reference pump

Note that if both pumps are the same pump, we can substitute from the Affinity Laws:

Q₂/Q₁ = N₂/N₁

Equation 13‑6 reduces to Equation 13‑3, confirming the 0.375 exponent.

If we choose to "normalize" S to 3,550 rpm and to, say, 1,000 gpm (per eye), Equation 13‑6 becomes:

S_n = S 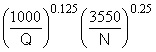                    (13-7)

     Where:

     S_n= Suction specific speed, normalized to 1,000 gpm and 3,550 rpm

     S = Suction specific speed established by testing (NPSHR for a 3 percent head drop)

     Q = BEP capacity of pump (per eye), GPM

     N = Test speed, RPM

 

References

1. Lobanoff, Val S. & Ross, Robert R., Centrifugal Pumps: Design & Application, Gulf Publishing, Houston, Texas, 1985.

2. Yedidiah, S., "Factor Pump Size into NPSH Comparisons," Power, June 1973.