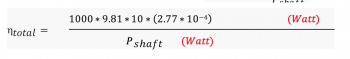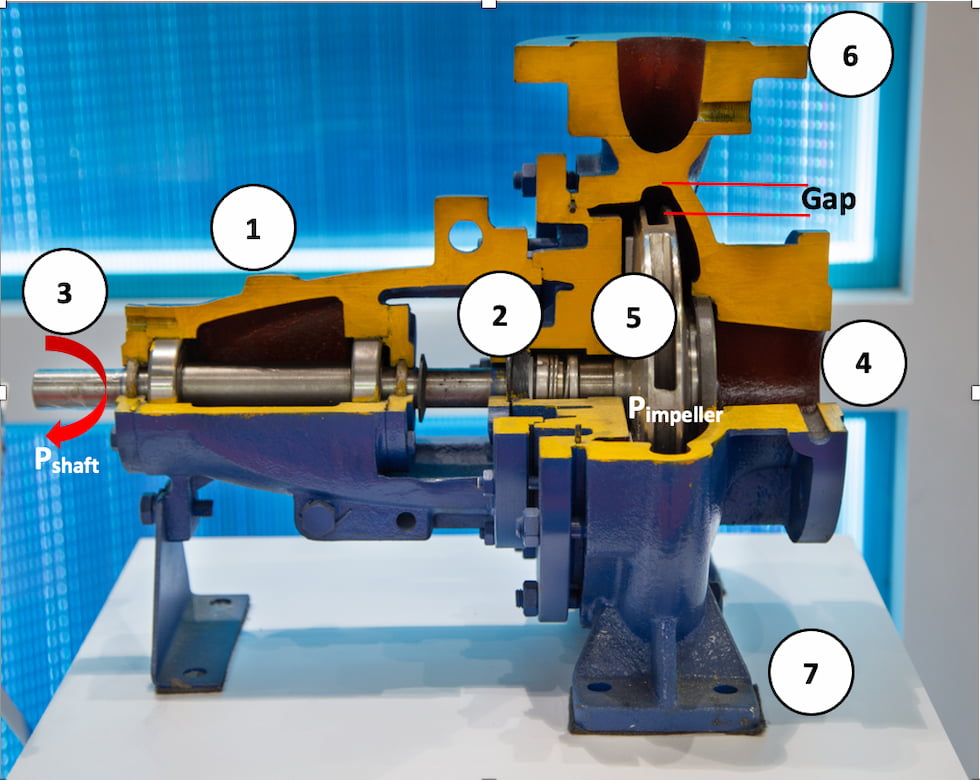
Imagine any type of pump; it has a driver to transfer the power to the pump shaft and a coupling, which connects the driver to the pump shaft. Outside the entrance of the pump structure, there is a bearing housing, which contains bearings to withstand applied forces to the pump shaft.
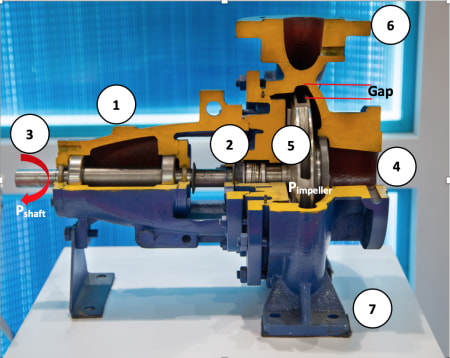
Beyond the bearing housing, there is a sealing region (Images 1 and 2). It is good to note that in both bearing housing and sealing, mechanical losses are inevitable.
There are three types of efficiencies in pumps:
1. Mechanical efficiency
2. Hydraulic efficiency
3. Volumetric efficiency
Mechanical Efficiency
After we push the start button of the pump, the driver will run and start to transfer mechanical power to the pump shaft. As illustrated in image 2, between the driver and pump shaft there is a coupling, which incurs some loss of power.
So now, the pump shaft has received power from the driver, needs to transfer it directly to the impeller and finally send it to a pumping medium, but as mentioned before, there will be some losses on bearing housing and on the sealing area.

Now we can understand the scenario in which power absorbed by the impeller is less than the power produced by the driver. For power that is absorbed by the pump shaft, we will use “Pshaft,” and for power absorbed by the impeller, we will use “Pimpeller” as a symbol for calculations.
What is Efficiency?
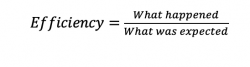
Now, if we want to put our parameters in the formula (Equation 2), we can do so. We were expecting that all Pshaft will transfer to the impeller, but in reality, P impeller must be considered because of the mentioned losses.
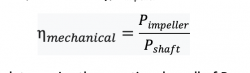
After this step, now let us raise the question: has all of P impeller been transferred to the pumping medium or not? To answer this question, we shall explain the second type of efficiency, which is hydraulic efficiency (
Hydraulic Efficiency
Using Equation 1, we know that the denominator (what was expected) is P impeller. For the numerator (what happened), we need to use the first and second law of thermodynamics. If you apply the laws of thermodynamics, we will arrive at the following equation (Equation 3).

What do we mean by “Q” in Equation 3?
In this section (Equation 4), we assume that all of the input flow (Q) has exited the pump discharge nozzle (image 1). This is denoted by “Qtotal”.

Volumetric Efficiency
In Equation 4, we assumed that all the flow that enters the pump also exits from it. So in other words, Qinlet = Qoutlet. However, is this a true assumption?
This is definitely not true because inside of the pump, there are a lot of gaps, like the gap of the tip of an impeller with casing, the gap between wear rings, etc. Therefore, there is always some amount of leakage. This means that Qinlet > Qoutlet (Equation 5).

For the case of simplicity, we can replace
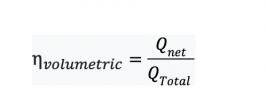
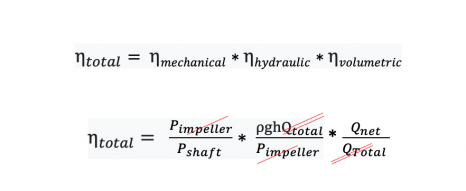
Now that we have all three efficiencies, you might ask, what is the total efficiency of the pump?
Let us try to multiply all three efficiencies together (Equation X).
Finally, we end up with (Equation 7)
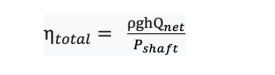
As you noticed, understanding efficiencies in pumps are not so hard.
Units Used:
PShaft = power absorbed by pump shaft (kW)
g = Acceleration due to gravity = 9.81 m/s2
h = differential head (m)
Q = Flow rate (m3/s)
P = Power (Kw)Example:
1 m3/h of water is pumped a head of 10 m. Calculate the total efficiency of the pump.
We will use this formula:
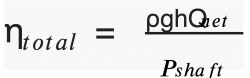
Given (Equation 8):
ρwater = 1000 𝐾𝑔/𝑚3, Q = 1 m3/h, but we should convert to m3/sec. The conversion factor is 3600 Therefore, 1 m3/h = 1/3600 m3/sec = 2.77 x 10-4 m3/sec, H = 10 m, g= 9.81 m/s2
Now put this data into the formula (Equation 9, then Equation 10):
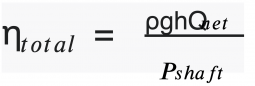
Please note that the unit for the nominator of the above equation is in Watts, and if you want to convert to kW (kilowatts), you should divide it by 1000.