Under Pressure: The Dangers of Vapor Pressure

This month’s column is not about the Queen rock song made famous by David Bowie. Instead it highlights an issue that is common in the pump industry—misunderstanding the concept of vapor pressure. In recent weeks, I have been asked to solve several pump issues that resulted from a misunderstanding of vapor pressure. The first case involved a self-primer pump lift application where the fluid was water at 150 degrees Fahrenheit (F). The second case involved confusion regarding net positive suction head available (NPSHa) on a condensate pump. The pump suction pressure was 134 pounds per square inch (psi). Consequently, the user incorrectly assumed there was no need to calculate the NPSHa.

Self-Primer Pump Application

In the first case of the self-primer pump misapplication, I offer two examples to illustrate this suction lift application. We refer to this as a lift application because the surface level of the fluid supply is below the centerline of the pump impeller. For a self-primer pump in a lift application, understand that the pump does not reach out and pull or suck the fluid into the pump. There must be some external force that causes the fluid to flow to the pump suction. In most cases with self-priming pumps, it is atmospheric pressure pushing down on the fluid that supplies the energy to push the fluid to the pump impeller. Because the acting force is atmospheric pressure, the maximum amount you can supply depends on the elevation of the pump relative to sea level. However, there are instances where it is possible to be below sea level, such as Death Valley in California (282 feet below sea level) and the Dead Sea in Israel (1,300 feet below sea level), to name two well-known examples. Just as with any pump application, the NPSHa calculation must be performed to make sure there is sufficient margin above the net positive suction head required (NPSHr). If the margin is not sufficient, the pump will cavitate, damage will occur and the pump performance will drop off or fail altogether.

NPSHa

First, let us review the formula for NPSHa and recognize that a key factor in the equation is the head from vapor pressure. Note that vapor pressure will always be a negative value in the NPSHa equation, so it is also a factor that will always work against you. As I tell my pump students, “vapor pressure is never your friend.” A simple formula for NPSHa is shown below, where the units are expressed in absolute feet of head. Since this is a lift condition, the static head component will be a negative value.

Two Versions of a Self-Primer Example

In both versions, the application is identical, except the temperature of the fluid is higher in the second version. The higher temperature means the vapor pressure has increased. In each version, the suction lift is 10 feet, the friction loss is 3 feet and the site elevation is at sea level. Positioning at sea level means the absolute pressure rounds out to 34 feet of head (14.7 psi absolute atmospheric pressure x 2.31 divided by the specific gravity of 1.0 = 33.96 feet ≈ 34). In the first version, the fluid is water at 68 F, and in the second version the fluid is water at 150 F. When you look up the vapor pressure of water for each temperature, note it is normally expressed in pounds per square inch absolute (psia), so you must convert that value to feet (head) to have the component value in the proper units needed to do the NPSHa calculation. To convert psi to head, you must multiply by 2.31 and divide by the specific gravity for that temperature. For the first version of 68 F water, the specific gravity is 1.0 and the vapor pressure is 0.33889 psia. For the second version of 150 F water, the vapor pressure is 3.7184 psia and the specific gravity is 0.9802. You can find the vapor pressure and specific gravity values in several places. I use the “Cameron Hydraulic Data Book,” and there are also several reputable web-based sources. Once you have the conversions, fill in the values for the formula and do the simple math steps (0.33889 X 2.31 = 0.783 feet. And 0.783 divided by 1 remains = 0.783). Then, fill in the values in the NPSHa formula and complete the steps for the answer. Repeat these steps using the higher temperature values for version 2.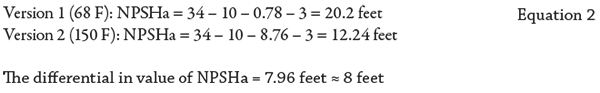 In summary, all the parameters except temperature (vapor pressure) are the same, and simply changing the temperature of the fluid from 68 F to 150 F reduced the available NPSH by almost 8 feet. This may not seem like a big deal, until you realize that the pump requires 13 feet of NPSH at the condition point and 12.24 feet is all that is available. At this NPSHa value, the pump will not operate correctly and will be in a constant state of cavitation. Anytime you have a self-primer pump (or any pump) application, you must calculate the NPSHa, which also means you need to know how to calculate the negative head from vapor pressure. Most manufacturers do not recommend using self-primer pumps on lift applications above 145 F for this very reason. The workable solution for higher temperatures will likely involve a submersible or a vertical sump pump.

High Suction Pressure — Condensate Pump

The second case evolves from the misconception, “If you have high pressure on the pump suction, then there is no need to calculate the NPSH.” Again, vapor pressure is not your friend, and as fluid temperature rises, the corresponding rise in vapor pressure will erode any benefit from the high suction pressures. I have unfortunately witnessed this mistake countless times over my career. A common steam system supplies saturated steam at working pressure and temperature for the processes in the facility. After the steam does its work as part of the system process, it is condensed to liquid (condensate) and later reheated to repeat the steam cycle. The condensate is normally collected in a tank or “hot well” that can be at a pressure above ambient or in a vacuum. The example we will look at involves deaerator tanks at some pressure above ambient. Deaerator tanks are primarily used on commercial and industrial steam systems as a method to remove oxygen, carbon dioxide and other noncondensable gases from the system. They serve many other purposes, but oxygen removal is the primary goal so that system corrosion is mitigated. To force the gases from solution, the fluid is heated to an equilibrium condition. This means the water will be at its saturation point (the fluid is at its boiling point), which also means the vapor pressure will be equal to the pressure in the deaerator tank. Looking at the NPSHa formula above, note that the head (pressure) from the absolute pressure will be equally countered by the head (pressure) of the vapor pressure component. In short, they will negate each other. In this example the pump suction pressure is at approximately 134 psia, and the fluid is water at 350 F. This is a common situation with 150-pound steam systems. The error that occurs is when the pump system owner looks at this pressure and incorrectly thinks they have so much excess suction pressure there is surely no need to calculate the NPSHa. The problem as in the previous example is that the feet of head from the vapor pressure will negate every foot of head from the absolute pressure. Again, using the NPSHa equation, fill in the components for this example: The static head will be 10 feet, and the friction value will be 3 feet. The absolute suction pressure is 134 psia (converted to head becomes 350 feet). Note: I am rounding, so numbers will be off slightly. The vapor pressure for 350 F water is also 134 psia, so it cancels any gain from the suction pressure (head). Since this is a flooded situation where the fluid level is above the pump, the static head is a positive value.

Vapor Pressure Explained

Due to the confines of this article, we will only discuss vapor pressures for liquids that are not derived from hydrocarbons or mixtures such as gasoline. You should consult a reliable technical reference for a more thorough explanation of vapor pressure.

• Vapor pressure is the pressure required for a liquid to boil at a given temperature.
• Each liquid has its own unique vapor pressure values and characteristics.
• The vapor pressure of a liquid will increase with temperature and vice versa.
• The vapor pressure of a liquid at a given temperature is the pressure that it will flash (change state) to vapor if heat is added.
• The opposite is also true—the pressure where the vapor at a given temperature will condense to liquid form if heat is removed.
• The surface area of the liquid has no effect on the vapor pressure.
• Equilibrium is when the evaporation rate of the fluid is equal to the condensation rate measured at the surface where the fluid (liquid) and the atmosphere (gas) meet.
• When the vapor pressure is equal to the atmospheric (or ambient) pressure that will be the boiling point.
• Saturation temperature means boiling point.
• The saturation temperature is the temperature for a corresponding saturation pressure at which a liquid boils into its vapor phase.

Any liquid in an open container will evaporate to a vapor unless some other force is present to prevent the change from occurring. In most examples, that force is simply atmospheric pressure. The fluid exerts a certain pressure to the atmosphere and in return the atmosphere exerts a counter pressure. For water below 212 F, the atmospheric pressure is greater than the vapor pressure. Those two pressures (liquid and atmospheric) would be in equilibrium if the water was at 212 F at sea level where the water would begin to boil. If you were at higher elevations (lower ambient pressure) the water would boil at a lower temperature. For instance, at 10,000 feet above sea level, water would boil at about 194 F. A slightly different way to think of vapor pressure is to equate it with the boiling point for that liquid at some pressure. Just keep in mind that, in reality, it is more complicated. As previously mentioned, water at room temperature and pressure will not vaporize until you raise the temperature to 212 F. However, you can also boil water at room temperature by reducing the pressure. For 68 F water the boiling point could be obtained by lowering the pressure to 0.34 psia. Note this value of absolute pressure is approaching an extremely high level of vacuum, so this does not often occur except in special processes.

Conclusion

Why are we discussing this subject at all? Because cavitation occurs in the pump when the fluid pressure drops below its vapor pressure. This phenomena can occur by either increasing the temperature or reducing the pressure, but in almost all cavitation cases it is because the lowest pressure the fluid will experience in the pump system is the area immediately in front of the impeller eye. If the pressure is below the vapor pressure, it will flash to vapor—not because of a temperature change, but because of a pressure change.