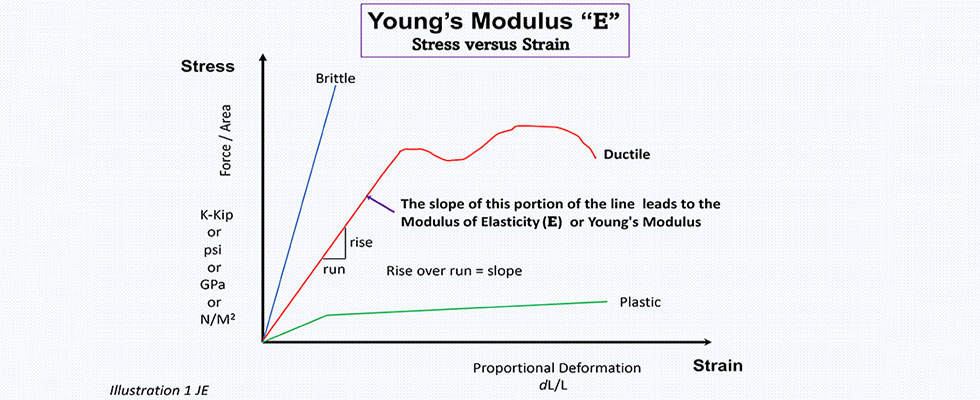
IMAGE 1: Expression of Young’s Modulus (Images courtesy of the author)
I frequently talk with pump owners who believe the root cause of shaft failure is solely the strength (or lack thereof) of the material. I offer this column as a counterpoint discussion on the subject.
In my February 2017 column, I discussed the major reasons why shafts on overhung pumps break in service. Normally the shaft will break because the pump is being asked to do something it was not designed for. Root cause failure analysis (RCFA) typically reveals fatigue failure due to excessive shaft deflection. Fatigue failure is also known as failure due to reversed bending fatigue with rotation. Shaft deflection is the preventable result of operating the pump in the wrong area of the curve and/or poor maintenance choices. There are a few exceptions to this common failure mode such as metallurgical defects and/or errors in the manufacturing process.
Mistakes do happen, but for most manufacturers they occur at numbers statistically approaching Six Sigma levels. That is 3.4 defects per 1 million opportunities (DPMO) or think of it as 99.99966% of all the shafts are made without a defect. Reducing shaft deflection will manifest in longer pump life, reduced cost of ownership and higher reliability.
Shaft Design
There is a long list of requirements to consider when designing pump shafts. All credible pump manufacturers that desire to remain in business will design the shafts for normal startup and operational factors, albeit a smaller number will have higher margins for upset conditions and safety margins in general. Economics will drive the key parameters that the designer must take into consideration, which at a minimum include torque, speed, various stresses such as key-seat geometry and placement, fillet radius, surface finish, hydraulic load, component weight, and bearing placement/span.
As added emphasis, I want to point out that shaft diameter is determined mainly by the amount of torque expected/required. Pump shaft design presents difficult calculations and manufacturing choices due to the various diameters required to accommodate the components for assembly and maintenance.
In addition to the above factors, before you decide on a shaft material for your application, consider the temperature, pH and the percentage of suspended solids in the pumpage. Please refer to my February 2017 column and/or listed references for more specific information.
Materials
Common shaft materials include austenitic 304 and 316 stainless, martensitic 410 and 416 stainless, CD4MCu duplex steel, carbon steels 1040 and 1045, alloy steel 4140 and precipitation hardened martensitic stainless steel 17-4 PH. Your pump shaft may be of a different material but it will likely have similar mechanical, thermal, electrical and chemical (alloy composition) properties.
Additionally, realize that all materials are elastic to some degree. We can easily understand this concept when considering elastomers such as rubber and plastic, but we rarely think of elasticity when it comes to metals—yet all metals are elastic.
Young’s Modulus—What Is a Modulus?
The word modulus has Latin roots and, with sincere apologies to my Latin teacher Mrs. Bruenig, roughly translated it means to measure or gauge. In the field of mathematics, it is another term for absolute value. In physics, modulus is a constant factor or ratio. In computer science it means something else. In metallurgy, we think of it as the ratio of two different curve slopes.
Note: For material science, there are three types of moduli.
Bulk modulus: The ratio of stress to the fractional decrease in the volume of the body or a measure of how resistant the material is to compression.
Shear modulus: The ratio of tangential force per unit area to the angular deformation of the body or how resistant a material is to shearing deformation. Shear modulus is the ratio of shear stress to shear strain.
Very closely related and for this column elastic modulus (aka Young’s modulus): Young’s modulus is the ratio of tensile stress to tensile strain or the ratio of longitudinal stress to strain.
For our general purpose and in layman’s terms, we can think of Young’s modulus simply as a ratio (technically a ratio would not have units), and more importantly, that it tells the pump designer whether the shaft material will bend, deform or break given some amount of stress.
Young’s modulus is expressed as E. Where E = stress ÷ strain. (Where stress is simply the force per unit area and strain is the amount of differential change [deformation] in the length.)
See Image 1.
Young’s modulus is a measure of elasticity and should not be confused with strength, toughness or hardness. Since the most common shaft materials all have a similar value of Young’s modulus, the decision to change materials due to some deleterious issue is rarely in and of itself the solution to correcting the root cause of shaft failure. The various shaft material choices will have different properties for corrosion resistance, hardness and tensile strength, and a specific selection may work better for your application—if the shaft is not deflecting excessively.
Young’s modulus is, in essence, the elastic property of the material—that is, how many times can you bend it before it breaks? Elasticity is a material property indicating how it will restore it to its original shape after distortion. Technically, and more importantly, is how far can you bend it on each cycle over hundreds of thousands of cycles before you exceed the limits of the material? This is also known as the “endurance limit” and when a shaft does break, we in materials engineering jokingly (nerd humor) refer to this as accidentally exceeding the “Goodman Line.”
If you investigate the eight most commonly used pump shaft materials, you will see some differences in the properties of hardness, strength and corrosion resistance. What you will also notice is that the value of Young’s modulus for all the materials fits tightly in the same range. The one exception would be titanium, which has a higher value.
Average values for Young’s modulus in imperial U.S. customary units (pounds per square inch [psi])
316-SS 29.0 x 106 psi
17-4 PH 28.0 x 106 psi
4140 28.5 x 106 psi
CD4MCu 29.0 x 106 psi
For SI units (metric international system of units), the value of the psi units would convert to approximately 190 to 195 gigapascal (GPa). Sometimes the units are expressed as Newtons per square meter (N/m2).
Shaft Deflection (Bending)
Shaft deflection in an operating pump is a result of three main factors. The first is that the shaft is bent in the first place. Any shaft with more than 0.0025-inch to 0.003-inch runout should be replaced.
The second reason is rotor imbalance. Imbalance is typically not an issue with the shaft but it will be with the impeller, which is why it is always a smart idea to balance the impeller. Balance to at least International Organization for Standardization (ISO) 1940 grade 6.3 or better. Shaft deflection from an unbalanced impeller is referred to as “whip.”
The third reason is unmitigated radial thrust from operating the pump away from the allowable/preferred operating zone (A/POZ). Note that all three of these issues can manifest at the same time.
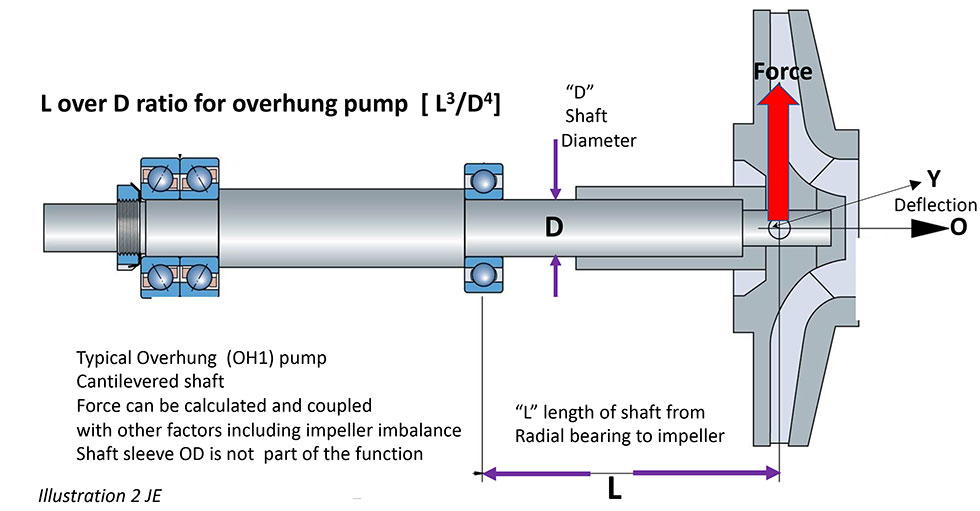
One simple step to reduce deflection would be to use solid shafts in lieu of sleeved shafts. Of course, that requires a shift to cartridge-type mechanical seals and not all operators and applications can accommodate this decision. Additionally, many pump manufacturers offer options for larger diameter shafts to mitigate deflection. Reducing deflection not only saves the shaft from fatigue failure but also prolongs mechanical seal life. Most seal manufacturers require less than 0.002-inch deflection at the seal face to have a successful seal life. See my February 2016 column for more details. An added benefit of reducing deflection is prolonged bearing life.
Realize that shaft deflection occurs two times for every one revolution of the shaft. Consequently, a pump operating at 3,550 rotations per minute (rpm) will deflect 7,100 times per minute. For details on calculating radial thrust, refer to my column devoted to this subject in January 2021.
Shaft Deflection Factor
One last and most important factor for overhung pumps is the amount of shaft cantilever and corresponding deflection simply known as the “L over D ratio” of the shaft (properly stated as L3 ÷ D4 or L3/D4). Where L is the axial distance from the impeller centerline to the center of the radial bearing and D is the diameter of the shaft. The ratio is derived and simplified from the cantilevered beam deflection formula used in statics. I am not going to derive the formula in this column, but I will broadly illustrate the relationship and point out that a major factor in the deflection formula is the modulus of elasticity E (Young’s modulus). It is a much more complicated calculation/derivation.
See Images 2 and 3.

The L/D ratio is also called the “slenderness ratio” or “shaft stiffness ratio.” It is an indication of how much the shaft will deflect (bend) due to radial hydraulic forces when the pump is operating away from the design point (best efficiency point or BEP). The L over D ratio is really only applicable to overhung pumps.
I postulate that shaft failure cannot be prevented simply by material choices but it can be mitigated by geometric decisions.
The most common form of shaft failure is fatigue. The fatigue is due to excessive shaft deflection, which is a function of the radial hydraulic loading, rotor balance and the shaft stiffness. The strength of the shaft has little to no effect on the stiffness. The stiffness is a function of the modulus of elasticity (Young’s modulus) and the L over D ratio (geometric dimension).
Common shaft materials all fall into a tight range of values for Young’s modulus (29 x 106 psi). Consequently, only changing shaft materials to preclude/mitigate shaft breakage is not necessarily a prudent decision. You will experience higher pump reliability if you address the root cause operational factors.
References
Mechanical Engineering Design (5th Edition), Joseph Shigley and Charles Mischke
Root Cause Failure Analysis—Understanding Mechanical Failures, Neville Sachs
How Components Fail, (ASM publication) Donald Wulpi
Statics (Mechanics for Engineers) 3rd Edition, F. Beer, and E.R. Johnson
API Standard 610 (11th edition) Annex K

