This is the second article in a five-part series. Read the first part of the series here.
Last month, we worked through an example for a simple system calculation of net positive suction head available (NPSHa) based on a 10-foot flooded suction with 68 F water at sea level. The head due to friction in the suction system was 3.2 feet. After working through the formula with the data (calculated or given), the answer for the amount of NPSHa was 40 feet.
This month, we will turn the suction system around and calculate the NPSHa for a 10-foot suction lift. The liquid source will remain open to atmospheric pressure. The location elevation is at sea level and the liquid is water at a temperature of 68 F. The friction head (hf) for the suction side system is calculated by the author at 3.2 feet. Please refer to Image 1 (Example 2 for this series) to see the system arrangement for this second example.
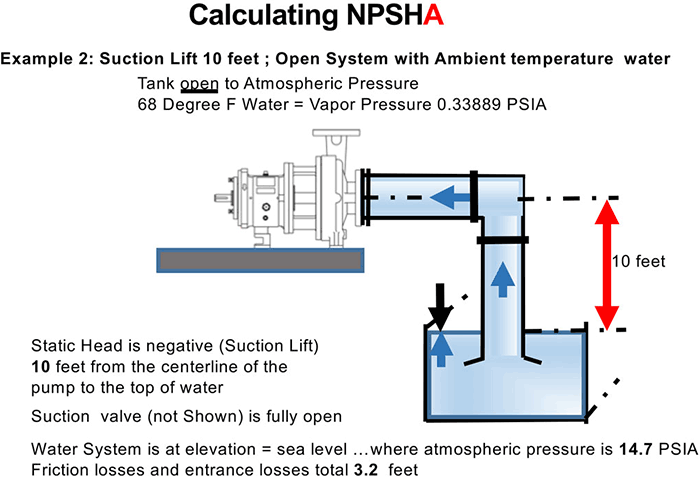 Image 1. The system arrangement for a 10-foot suction lift. (Image courtesy of the author)
Image 1. The system arrangement for a 10-foot suction lift. (Image courtesy of the author)We call this a “lift” situation because the top surface of the liquid is below the centerline of the pump impeller. Consequently, the static head will be a negative quantity. The pump is not really “lifting” the liquid because water (along with all other liquids) has no tensile strength, and the pump is not capable of reaching out and pulling the fluid in—a common misconception. Due to atmospheric pressure pushing down on the fluid, there is a force that causes the liquid to move to the pump when the air in the line is removed (the pump is primed). The pump exerts a small amount of differential pressure on the liquid in front of the impeller that initiates flow.
The actual suction lift is the static head plus the friction head that must be overcome. In this case, the static head is 10 feet and the friction head is 3.2 feet, so the actual suction lift added together is 13.2 feet.
When calculating the power required to drive the pump, you need to consider the work done in the lift evolution, because the pump is moving liquid of a certain weight per unit volume up a vertical distance (lift or static suction lift). Water at 68 F is 62.32 pounds per cubic foot or 8.33 pounds per gallon.

As I said last month, the formula for NPSHa is my “friend” because if I can fill in the values for the formula, then all I need to do is the math to get my result (also known as “plug and chug”). The formula for NPSHa for a suction lift condition is in the box above.
Notes:
- (ha) The system is open to atmosphere so the absolute pressure above the liquid in this example is simply atmospheric pressure. The pump site location/elevation was given as sea level. Consequently, the absolute atmospheric pressure at sea level of 14.7 pounds per square inch absolute (psia) can be converted to feet (absolute) by simply multiplying 14.7 psia by 2.31. The answer is 33.957 feet, rounded to 34 feet for this illustration. For elevations above sea level, the absolute pressure (head) will be reduced proportionally with the increase in elevation. Look at reference charts that will provide this information. Also, be aware there are locations that may be below sea level.
- (hvpa) The head due to the vapor pressure is a direct function of the liquid properties and its temperature. With water at 68 F, you can look up the vapor pressure in a reference source such as the “Cameron Hydraulic Data Book” and it is usually expressed in units of psia. The 68 F water will have a vapor pressure of 0.33889 psia, which will convert to 0.7828 feet when you multiply by 2.31 and divide by the specific gravity (SG) of 1.0.
- (hst) The static head will be negative because it is a lift situation, meaning the surface of the liquid is below the centerline of the impeller. The difference in elevation is 10 feet.
- (hf) The friction head was given as 3.2 feet.
- (hvelocity) This is not shown in the equation. The velocity head is not required when calculating the NPSHa. It is accounted for elsewhere in the formula.
- You should always calculate for the worst condition. The liquid surface level may be a different (lower) level. The temperature of the liquid may be hotter, which will increase the head of vapor pressure. The friction head may also increase with time, fouling, corrosion or with different valve settings.
To solve for NPSHa, fill in the given or calculated values. Again, the static head factor is negative in this example because it is a lift condition, and for last month’s example the static head was positive because it was a flooded suction.
The NPSHa formula for a lift is:

Last month, the NPSHa result for the 10-foot flooded suction Example 1 was 40 feet. The only change made this month for Example 2 was that the flooded suction was changed to a 10-foot suction lift with the NPSHa result of 20 feet.
Recognize that simply changing the conditions from a 10-foot flooded suction to a 10-foot suction lift changed the NPSHa by a difference of 20 feet.
Velocity Head (hvelocity): To Be or Not To Be?
I wish to explain a point of confusion for many of the readers. (I am guilty for not being consistent with this practice across many of my articles.) The component of velocity head (hvelocity) in the NPSHa formula is not required when you are calculating NPSHa using the formula method, but it is required when you are measuring for NPSHa.
There are two methods for the determination of NPSHa—either the calculation method or the empirical measurement for NPSHa. The fifth component in the NPSHa formula is velocity head and must be included if you are (measuring) determining the NPSH from a gauge reading on the pump suction. Velocity head is already included if the NPSH is established from a difference in elevation. The velocity head component is a positive value when used in the equation.
Measuring NPSHa = head of inlet + head of velocity – head vapor pressure.
Head of the inlet is equal to the absolute head + or – the static head – the friction head.
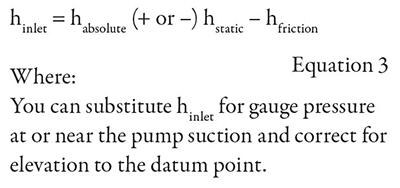
It is important to know that when measuring for NPSHa using a suction pressure gauge, the difference in elevation between the gauge and the pump impeller centerline (my proposed datum point for this example) must be corrected for the NPSHa result. If the gauge is above the datum point, add the result (how many feet or fraction thereof) and if the gauge is below the datum, subtract the elevation amount.
Most gauges used in the field are not accurate enough or in the wrong range/scale to measure for the specific purpose of NPSHa. Using a calibrated gauge in the proper range, with the proper scale, can yield good results.
References
Cameron Hydraulic Data Book, 16th edition
To read other articles in the 'Common Pumping Mistakes' column, go here.

