Columnist Lev Nelik says it is important to know when you can use a shortcut, and when to go the long way.
Pumping Machinery, LLC
01/02/2019
During our last Pump School session, one attendee asked how much error there would be if the velocity head and gauge elevation correction were not accounted for. While the most obvious answer perhaps would be “It depends,” we nevertheless went over a specific example with numbers to illustrate, as presented below. Such examples are numerous for relatively basic fluid transfer from one tank to another, or from a tank to a process. Let’s take a typical single-stage pump, operating as shown on a performance curve in Image 1.
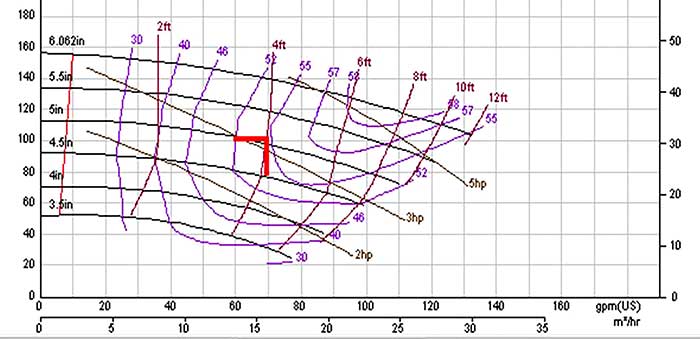 Image 1. A pump performance curve with operating point noted
Image 1. A pump performance curve with operating point noted
To read more Pumping Prescriptions columns, click here.

