Horsepower and fluid movement
by Jim Elsey
03/14/2018

Editor’s Note: In the February 2018 issue of Pumps & Systems, we covered the simple physics and conservation of energy phenomena occurring in the pump casing, where the impeller-generated fluid velocity is converted to pressure in the pump casing. We also discussed why pump manufacturers use the term “head” while operators will be concerned with pressure. The simple explanation for using head instead of pressure is that the pressure from a pump will change if the weight/specific gravity (SG) and or temperature of the liquid changes, but the head will not change. We also covered how most pump problems occur on the suction side and that you should always operate a pump as close to the best efficiency point (BEP) as is possible.
Specific gravity (SG) is a ratio of two different fluid densities. We use the SG (1.0) of water as the base fluid, so we are comparing all other liquids to water. SG equals density of a liquid divided by the density of water. Since every fluid can have a different SG due either to its inherent properties or the temperature when it is being pumped, pressure is not a convenient method to select and size the pump. However, since the developed energy/head is predictable and constant regardless of the fluid pumped, industry professionals use head to describe/predict the pump performance. Also when using head, we can provide one performance curve per pump for different fluids at different temperatures. If we used pressure, we would need an infinite number of curves. Most pump performance curves are based on water at approximately 68 degrees Fahrenheit (F). If you are pumping a fluid other than water, please consult with the manufacturer to have them “correct” the curve for the fluid you will be pumping. 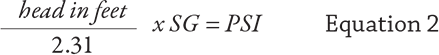Equation 2 Equations 2 and 3 show how to convert from head to pressure or vice versa. 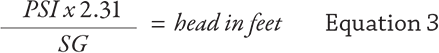Equation 3 For an example, consider three identical pumps each pumping a different fluid. Each pump has the same impeller diameter, the same speed and the same system curve. Pump A is pumping water with a SG of 1.0. Pump B is pumping a light hydrocarbon with a SG of 0.7 and pump C is pumping an acid of SG 1.23. Assuming all three pumps were rated for 115 feet of head, they would produce 50 pounds per square inch (psi) for pump A, 35 psi for pump B and 61 psi for pump C, but all three pumps would produce 115 feet of head. An antithesis example would be if the pumps were selected and rated for 100 psi. Then pump A with a SG of 1.0 would produce 231 feet of head, pump B with a SG of 0.7 would produce 330 feet of head and pump C with a SG of 1.23 would produce 187 feet of head. I am frequently asked where the conversion factor 2.31 derives from. A 2.31- foot vertical column of water at ambient temperature (SG of 1.0) will indicate 1 pound of pressure on a gauge at the base. Note this will vary slightly with temperature and gravitational field. 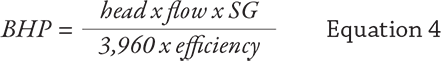Equation 4

Horsepower

It requires a defined amount of power to pump a defined amount (weight) of fluid to a selected height or distance within a fixed unit of time requires a defined amount of power. We can see the relationship by looking at the formula for calculating brake horsepower (BHP). See Equation 4. For centrifugal pumps in US-C units:
  • head in feet
  • flow in gpm
  • efficiency expressed as a decimal
In the formula, flow and head both have a direct relationship on the horsepower required. Any increase in flow or head will increase the horsepower. The opposite is also true. The SG also has a direct relationship on the outcome. The efficiency of the pump is expressed as a decimal and is the efficiency at the selected head and flow in the numerator. You will need to determine this efficiency from the manufacturer’s performance curve. Note the inverse relationship with efficiency. An increase in efficiency will reduce the required horsepower. Final note on this algebraic formula for BHP: it can be solved for any one unknown if you know the other variables. For example if you already knew the BHP, but did not know the efficiency, you could set up and solve for that unknown. In the field, I frequently use this formula to solve for the flow rate.

How Does the Fluid Get to the Pump?

Many people mistakenly believe that centrifugal pumps suck the fluid from the suction source. There must be some other energy source to deliver the fluid to the suction eye of the impeller. Fluids have no tensile strength, and the impeller is not capable of reaching out to pull the fluid into the pump (regardless of manufacturer). From a full bucket of water, reach in and grab the water with your hand and attempt to pull/lift the fluid to another container, and all that happens is your hand gets wet. Note of acquiescence: When the pump impeller is turning at operating speed, the fluid velocity is changing in front of the impeller eye. This velocity change does induce a small differential pressure at the inlet of the impeller. Some other force must move the liquid in the suction system to the impeller eye. Often, this other force is gravity because the source of supply is at a higher elevation than the pump suction. There may also be pressure involved. In the event of a lift situation where the pump is above the source of supply, it is atmospheric pressure pushing down on the fluid surface that supplies the energy. The limits of atmospheric pressure as a suction supply force therefore are 34 feet of “lift” if the pump is at sea level. Atmospheric pressure is 14.7, and 14.7 psi X 2.31 is about 34 feet. However, due to friction, imperfect systems, air ingress and liquid vapor pressure, most pump lift capabilities are limited to 25 feet or less. References Cameron Hydraulic Data Book
To read other articles in the 'Common Pumping Mistakes' column, go here.



Jim Elsey is a mechanical engineer who has focused on rotating equipment design and applications for the military and several large original equipment manufacturers for 43 years in most industrial markets around the world. Elsey is an active member of the American Society of Mechanical Engineers, the National Association of Corrosion Engineers and the American Society for Metals. He is the general manager for Summit Pump Inc. and the principal of MaDDog Pump Consultants LLC. Elsey may be reached at jim@summitpump.com.

Issue

March 2018