03/28/2014
Last of Two Parts
In Part One of this series (Pumps & Systems, February 2014), the operating and maintenance costs for pumped systems were isolated. The next steps are to set realistic goals for the proposed system improvement program, define the energy and maintenance saving objectives, improve the system uptime and calculate the potential savings.
Realistic Goals
Setting the goals for the program is critical. These goals provide a starting point for estimating the value of implementing a system improvement program. The plant’s financial management team must determine this information to calculate the risk versus the reward for proceeding with the program. In the vat dilution pump case study (Pumps & Systems, January 2014), we explored how correcting system problems can reduce the operating costs, maintenance costs and improved system uptime. When starting a pumped system improvement program, expect similar results.Energy Saving Objectives
One of the stated goals of the improvement program is a reduction of energy consumption. Knowing that pumped systems are typically oversized, establishing an energy reduction goal before proceeding with the proposed improvement program is important. In the last installment of this column, it was proved that adding a variable speed drive resulted in an operating cost savings of 60 percent on the vat dilution pump. This is a realistic number, and many systems in industrial plants can likely achieve even higher energy savings than 60 percent. However, it could be a bad idea to base financial justification for starting a pumped system improvement program on such high expectations. In this example, the energy savings goal is set at 30 percent. It is recommended to under promise and over deliver rather than not meet an excessively high goal.Maintenance Saving Objectives
Another goal of establishing a pumped system improvement program is reduction in maintenance costs. The vat dilution case study showed a direct relationship between energy savings and maintenance savings. Based on the direct relationship between power used and maintenance, a 30-percent reduction goal in maintenance costs can be estimated. Once again, this serves as a starting point for establishing the program.Increased System Uptime
The last stated goal for a pumped system improvement program is increasing system uptime. In the vat dilution case study, more than $400,000 in annual savings was attributed to an increase in the plant’s uptime. The improvement in plant uptime is a difficult number to estimate because of the interaction of the different plant systems. In this example, a 1 percent increase in system uptime will be estimated. A 1 percent increase in system uptime results in an additional 74 hours per year of manufacturing product. When starting a program, it is a good idea to establish a realistic goal while striving to increase the value of the program over time.
The Potential Savings
With the goals of the improvement program stated and the pump operating and maintenance costs estimated, the value of starting an improvement program can be calculated. The cost savings attributed to the improvement program are:- With the plant pump operating cost at $14.75 per ton of product produced, and a 30-percent estimate in energy-use savings results in savings of $4.40 in electrical power per ton of product.
- With the pump maintenance cost at $9.50 per ton of product, and a 30-percent reduction in maintenance cost results in savings of $2.85 per ton of product.
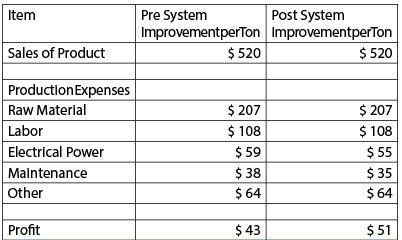 Table 2. The before and after financial balance sheet showing the estimated value of starting a pumped system improvement program based on the case study
Table 2. The before and after financial balance sheet showing the estimated value of starting a pumped system improvement program based on the case studyConclusion
This month’s article discussed how to estimate the financial benefits of starting a system improvement program within an industrial plant. Next month’s article will explain how to start a pumped system improvement program within an existing industrial plant.The Accuracy of Estimates
The financial justification for starting a pump system improvement program uses estimated data. The accuracy of any estimate is subject to question. This sidebar discusses the assumptions made and their validity for the estimates. The percent of power going into the motors that drive pumps is based on the design load on the motor control centers and switchgear. These numbers may be greater than the actual numbers because of the design margin used when sizing electrical loads. However, if the same magnitude of design margins for all electrical load calculations are assumed, the percentage of pump power to total power should hold true. When estimating maintenance savings, the same percentage is used as that of power savings. One may question the validity of basing the maintenance savings as a function of the power savings. However, pumped systems are typically oversized. Because of this, the following logic path describes how energy savings and maintenance savings are closely related:- Most pumped systems have a design margin used in pump selection, resulting in oversized pumps.
- Oversized pumps produce greater head than required by the system.
- Excess head requires additional electric energy to drive the pump.
- Excess energy increases the hydraulic energy of the process fluid.
- To control the system to a set value, a control valve must remove the excess fluid’s energy, resulting in heat, noise and vibration. This causes increased wear and tear on the components and increased maintenance costs.

