For a quick estimate of pump head in the field, the discharge pressure gauge is read. This number is multiplied by 2.31, and operators can get a rough value of the pump head. If the gauge reading is 80 psig gauge, then:
Head = 80 x 2.31 = 185 feet
Knowing the head and having a performance curve available, you can read back from the curve and have the flow. Many times that is a prime objective—to know, albeit approximately, the flow rate. Therefore, this method is acceptable.
However, while quick and simple, this method ignores many variables that could distort the answer. Some of these distortions can be insignificant, and others may greatly affect the number.
The Basics
Consider the basics: pump head is the difference between the total energies of the discharge side and suction side. This total energy has three components:
• Static head —a difference between the readings of the discharge and suction gauges, expressed in feet
• Velocity head difference
• Elevation difference—between readings of the discharge and suction gauges
A More Accurate Method
What would the results be if we attempt to compute this more accurately? How far would we be from the quick value of 185 feet of head?
Let’s look at another example. A pump moves 70 gallons per minute (gpm) of water, and the suction gauge reads 5 psig, and the discharge gauge reads 80 psig. The piping connected to the pump is 1.5 inches at the suction and 1 inch at the discharge. The suction gauge is 1 foot above the pump’s centerline. The discharge gauge is 6 feet above the pump centerline. What is the pump head with these numbers?

| Note: Can you confirm—for free registration to the next Pump School session—that 0.321 is a correct conversion constant to make the units come out correct? |
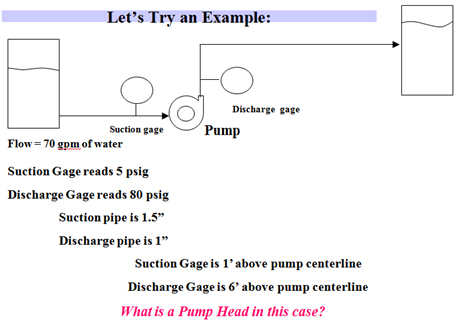
At the discharge, the area and velocity are:
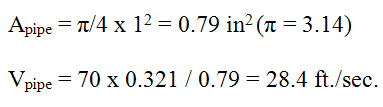
At the suction, the area and velocity are:
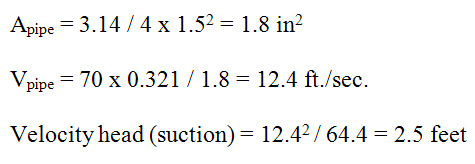
To get everything in consistent units (accounting for atmospheric pressure), in absolute units:

We came amazingly close—185 feet using the quick method versus 188 feet using the more accurate method—accounting for all the factors that can affect the calculation and spending extra time on the calculations). Does this mean that correcting for velocity head and gauge elevation is a waste of time? The answer to this question will be answered in the second part of this series in the September issue.
Readers Respond
.jpg) |
| Chuck Anderson’s answer |
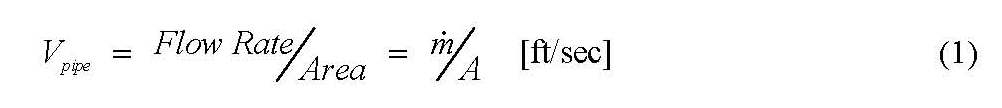 |
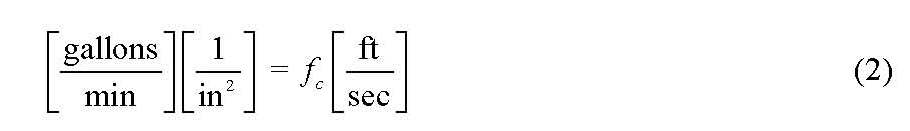 |
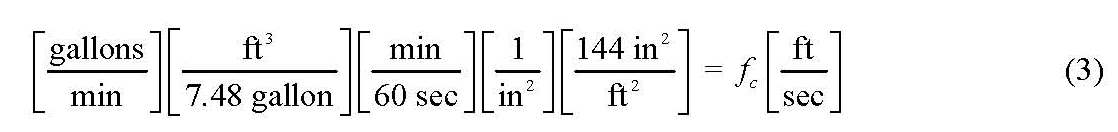 |
 |
Read part 2 of this story here.


