Understanding resonance is essential for solving problems of increased vibration.
Resonance is a condition that can occur in mechanical structures and can be described as sensitivity to a certain vibration frequency. Resonance occurs when a natural frequency is at or close to a forcing frequency, such as rotor speed. For machinery—such as pumps, turbines and electric motors—resonance can amplify the small vibratory forces from machine operation, and severe vibration levels can result. Such problems often develop after a speed change has been implemented, as with retrofitting a machine with an adjustable-speed drive (ASD) or operating a 50-hertz motor on 60 hertz of power.
The solution to these problems frequently depends on distinguishing between structural resonance and a rotor critical speed. Structural resonance refers to excessive vibrations of non-rotating components, usually machine components or supporting structures. Rotor critical speed refers to a condition in which the speed of the rotating element of the machine matches the rotor’s natural frequency.
Structural Resonance or Rotor Critical Speed?
Structural resonance is the more common resonant condition because of the complex design of the casing and supporting members. Most often the structure supporting a machine or a non-rotating machine component is resonant at or near the rotating speed of the machine. Even slight vibratory forces from residual unbalance and misalignment effects of the machine can excite the resonant base structure, resulting in severe vibration. A good example of structural resonance is the reed frequency vibration that often occurs with vertical turbine pumps that have a motor mounted on top of the discharge elbow. The machine components can also be resonant. There are many examples of two-pole electric motors where a resonant end bracket caused very high axial vibration at 1 x rpm or 2 x rpm.
A rotor critical speed exists when the resonant component is the rotating element of the machine. This is common with centrifugal pumps; gas and steam turbines; and large, two-pole electric motors. While the result is similar to structural resonance (high vibration when a certain operating speed is reached), rotor critical speed is a more complex phenomenon because of speed sensitive components, such as bearings. When the operating speed reaches the resonant frequency of the rotating element, the rotating element distorts, and the vibratory forces increase significantly.
It is important to properly distinguish between structural resonance and rotor critical speed. The term “critical speed” (without the word “rotor”) is somewhat ambiguous. Technically, a critical speed could be either a structural resonance or a rotor critical speed. For the sake of clarity it is best to avoid using that term. The simple term “resonance” can be applied to both conditions to avoid confusion.
The Characteristics of Resonance
As described above, the most notable characteristic of resonance is increased vibration when a certain operating speed is reached. Also, as the operating speed is increased beyond the resonant frequency, the vibration amplitude will decrease somewhat. The Bode plot in Figure 1 shows the operating speed versus the amplitude. For the sake of illustration, assume that the exciting force is residual unbalance of the rotor at the rotating speed.
The formula for calculating the natural frequency is:
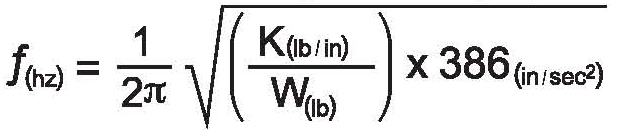
Where “K” is the stiffness of the resonant structure or component, and “W” is the weight (mass). Note that at the core of this formula is:
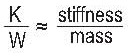
Increased stiffness will, therefore, raise the natural frequency, and increased mass will lower it. That is logical since stiffness creates a force that is always directed against motion, while mass has inertia, which is a force always directed with motion. Resonance is what happens when these two opposing forces are equal. They cancel each other out, allowing vibration to increase.
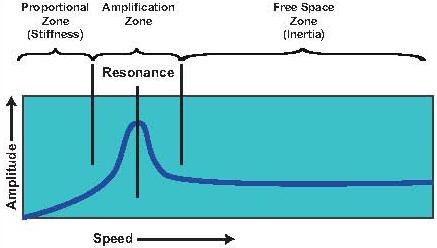 |
| Figure 1. Bode plot of resonance |
The Damping Factor
A third force, damping, is at work throughout the speed range. Damping absorbs vibratory energy, converting it to heat. In doing so, damping reduces the maximum amplitude of the vibration at resonance and increases the width of the amplification zone (see Figure 2). A common example of damping is shock absorbers on a vehicle. Machines with sleeve bearings may have significant damping that can even mask critical speeds. On machinery bases, concrete and grouting add significant damping to a base structure. These forces (stiffness, mass and damping) determine the characteristics of resonance and are important to the distinction between structural resonance and rotor critical speeds.
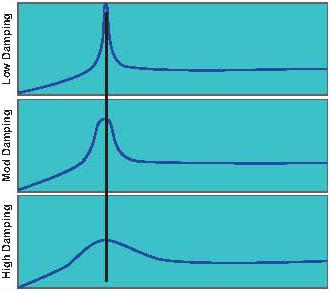 |
| Figure 2. The effect of damping on resonance |
With structural resonance, the machine operates close to a resonant frequency. It is most noticeable when damping is low, since high vibration amplitude results. Two rigid modes can be described as bouncing and rocking. Solutions include changing the resonant frequency to move it away from the operating speed by modifying the stiffness or mass and increasing damping to directly reduce the amplitude. (The different methods for implementing these corrective measures are topics for another article. The objective of this article is a comparison to rotor critical speeds.)
With a rotor critical speed, the problem is different. First, the stiffness, mass and damping of rotors mounted on rolling element bearings can almost never be effectively changed, and damping is typically very low. (Note: Mounted rotor natural frequencies of large journal bearing machines typically can be changed to some degree by modifying the bearing dynamics.) Second, no rotor is ever intentionally designed to have a critical speed close to its operating speed. The problem in this case is not that the operating speed is close to resonance, but that, at the rotor critical speed, the rotor distorts and non-linear effects cause excessive vibration. At that point, it becomes a flexible rotor rather than a rigid rotor.
A rigid rotor operates below the first rotor critical speed and may have numerous unbalance forces distributed along its axis. The sum of these unbalance forces can be corrected in any two planes with common, two-plane dynamic balancing methods. In these rigid modes, the rotor may flex slightly, but the motions at the bearings accurately represent the unbalance condition. However, once the rotor becomes flexible, above the first rotor critical speed, the distribution of unbalance forces will distort the rotor, causing an unbalanced condition that was not present in the rigid modes. This flexible mode unbalance causes increased vibration that persists at higher speeds.
With structural resonance, the force is constant while the vibratory response of the structure changes with speed. With a rotor critical speed, the force changes as the rotor distorts to conform to unbalance forces distributed along the axis of the rotor. The solution to rotor critical speed is to eliminate the unbalance forces in the planes along the axis of the rotor. Usually, it is not possible to detect where the unbalance forces are with the rotor in the rigid mode, so the rotor must be operated above the rotor critical speed (in the flexible mode) to detect the effects of the unbalance.
Bending Modes
As the speed of a rotor increases, it will go through a series of bending modes: first bending mode, second bending mode, third bending mode and so forth (see Figure 3).
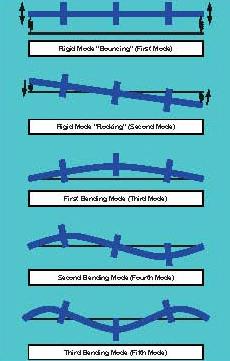 |
| Figure 3. Examples of a series of bending modes |
Rotors for multistage pumps and gas and steam turbines may operate above the first or second rotor critical speed, and generators sometimes operate above the third rotor critical speed.
Rotors for large, two-pole electric motors normally may operate above the first rotor critical speed but seldom above the second. Rotors that are designed for such flexible rotor operation have provisions for additional balancing planes to accommodate dynamic balancing procedures that eliminate the residual unbalance forces that cause flexible rotor distortion.
These dynamic balancing procedures may require that the rotor spin at operating speed, which can only be done safely with specially designed balancing machines in a spin pit. Alternatively, the individual components of flexible rotors, such as impellers, can be balanced before assembly.
Understanding the difference between structural resonance and rotor critical speeds will help clarify the discussion for maintenance and service personnel, especially when the topic is multistage pumps, turbines, or large, two-pole motors.

