Efficiency Matters
07/14/2016
A common concern in processing plants is determining the pumping health—or efficiency—of centrifugal pumps. As pump impeller seals wear as a result of erosion and corrosion mechanisms, tight internal clearances open up and allow fluid to recirculate internally, gradually degrading performance. As wear progresses, a centrifugal pump will eventually become unable to perform its intended function. Periodically monitoring pump performance allows end users to identify internal degradation before a serious loss of capability occurs.
The Old Method
In the past, plant machinery professionals have used the tried-and-true centrifugal pump horsepower equation (see Equation 1).
A Simplified Alternative
To sidestep these issues, a different equation can be used to determine centrifugal pump efficiency without having to know the liquid’s specific gravity and pump’s output shaft horsepower. This equation allows you to determine a centrifugal pump’s efficiency by only knowing these values: the pump’s discharge pressure (P2) and suction pressure (P1), flow rate (Q), electric motor efficiency (effm), and motor power in kilowatts (kW ). First, start with the basic hydraulic brake horsepower equation to eliminate the need to know the liquid’s specific gravity (see Equation 2)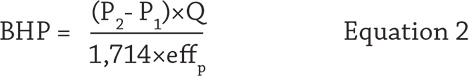

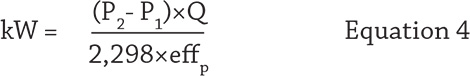
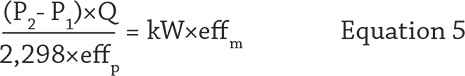

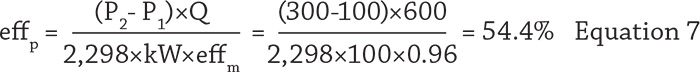
To read other Efficiency Matters articles, go here.

