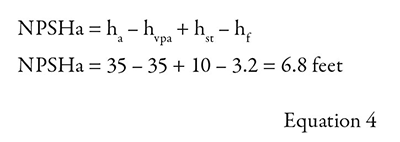Don't forget to take vapor pressure into consideration.
Summit Pump, Inc.
09/11/2018
This is the third article in a five-part series. Read the first part of the series here and the second part of the series here.
In the first part of this five-part series, we defined net positive suction head available (NPSHa) and walked through a simple calculation based on ambient temperature water for a flooded suction condition. In part two, we worked through an almost identical situation except the water source was at a level below the pump centerline, which is a suction lift situation. In both cases, the systems were open to atmospheric pressure, located at the elevation of sea level. The liquid temperature was at ambient 68 F.
Flooded Suction Pumping Hot Water
In this third part of the series, we will investigate what happens when the liquid temperature is above ambient. Before we get to the formula and the calculation, I recommend a review of the definition for vapor pressure. I covered vapor pressure in my April 2018 Pumps & Systems column should you wish to revisit. A brief summary is as follows. A liquid in an open container will eventually evaporate to a vapor unless some other force is present to prevent the change from occurring. In most examples, that force is simply atmospheric pressure. Even a bowl of water left on the kitchen counter will evaporate away over time, but it will happen at a significantly faster rate with each incremental increase in temperature. The amount of energy associated with the vapor pressure is subtracted from the total energy level available for the NPSHa. The energy associated with the vapor pressure is always a negative quantity. In the context of NPSHa, vapor pressure is not a friend to the pump. For a given temperature, a liquid exerts a certain pressure to the atmosphere, and the atmosphere exerts a counter pressure in return. For water temperatures below 212 F, the atmospheric pressure is greater than the vapor pressure. Those two pressures (vapor and atmospheric) would be in equilibrium if the water was at 212 F at sea level, where the water would begin to boil. If the pump example was at higher elevations (lower ambient pressure and consequently a lower equilibrium temperature) the water would boil at a lower temperature. Vapor pressures for water at various temperatures are easy to calculate or obtain in a reference source, but it is often very difficult to find reliable information on vapor pressures for other liquids. It is not uncommon for the end user/operator to be using the incorrect vapor pressure in their calculations.The Formula for NPSHa
Remember that we are calculating NPSHa, so we do not need to include velocity head. Velocity head would be included if we were measuring NPSHa. Please refer to Image 1.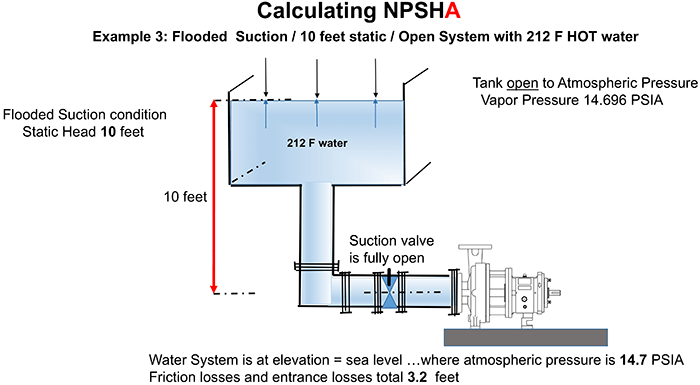 Image 1. Flooded suction with hot water (Image courtesy of the author)
Image 1. Flooded suction with hot water (Image courtesy of the author) For ease in working the example, I have calculated the total friction losses (hf) as 3.2 feet. Note that friction losses are technically lower for hot water than cold, but we will ignore the small difference for the examples in this series.
The tank is open to atmospheric pressure, and the system is located at an elevation of sea level. The absolute pressure in feet of head (ha) is 35.4 feet as a result. Remember from the formal NPSHa definition for absolute pressure (ha)… “is the absolute pressure as measured in feet of head of the liquid being pumped at the surface of the liquid.” Absolute atmospheric pressure is 14.7 pounds per square inch absolute (psia). To convert to feet, multiply by 2.31 and divide by the specific gravity of the liquid being pumped.
For ease in working the example, I have calculated the total friction losses (hf) as 3.2 feet. Note that friction losses are technically lower for hot water than cold, but we will ignore the small difference for the examples in this series.
The tank is open to atmospheric pressure, and the system is located at an elevation of sea level. The absolute pressure in feet of head (ha) is 35.4 feet as a result. Remember from the formal NPSHa definition for absolute pressure (ha)… “is the absolute pressure as measured in feet of head of the liquid being pumped at the surface of the liquid.” Absolute atmospheric pressure is 14.7 pounds per square inch absolute (psia). To convert to feet, multiply by 2.31 and divide by the specific gravity of the liquid being pumped.
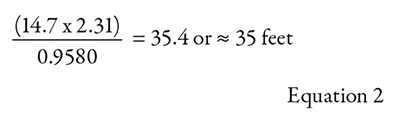 In real life examples, the actual atmospheric pressure will be slightly lower and vary with weather/barometric pressure and elevation above or below sea level.
Standard pressure at sea level may also be listed as 14.696 psia in lieu of 14.7. Either way, it rounds off to 14.7 psia. The more important fact is to know the actual elevation for the pump location and adjust your calculations accordingly.
The difference between this third example and the first example (see part one of this series, Pumps & Systems, July 2018) is that now the water temperature has been increased from 68 F to 212 F. Both examples are a flooded suction and an open system. Vapor pressure for 212 F water can be obtained from a reference text. Vapor pressure is normally expressed in units of psia, which must then be converted to feet (“for the liquid being pumped”) for use in the previous equation. The vapor pressure for water at 212 F is 14.696 psia. When converted to feet, this will round off to 35 feet.
The calculation is:
In real life examples, the actual atmospheric pressure will be slightly lower and vary with weather/barometric pressure and elevation above or below sea level.
Standard pressure at sea level may also be listed as 14.696 psia in lieu of 14.7. Either way, it rounds off to 14.7 psia. The more important fact is to know the actual elevation for the pump location and adjust your calculations accordingly.
The difference between this third example and the first example (see part one of this series, Pumps & Systems, July 2018) is that now the water temperature has been increased from 68 F to 212 F. Both examples are a flooded suction and an open system. Vapor pressure for 212 F water can be obtained from a reference text. Vapor pressure is normally expressed in units of psia, which must then be converted to feet (“for the liquid being pumped”) for use in the previous equation. The vapor pressure for water at 212 F is 14.696 psia. When converted to feet, this will round off to 35 feet.
The calculation is:
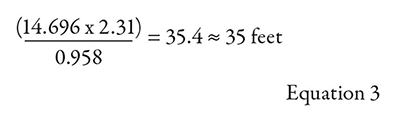 The significant difference for the current example is that the vapor pressure will be higher because the temperature is higher. The vapor pressure for 68 F water is 0.783 feet. (To obtain that value convert 0.33889 psia to head by multiplying by 2.31 and dividing by specific gravity, which was 1.0.) But now the vapor pressure for 212 F water is 35 feet. See Equation 3. This is a significant difference of almost 34 feet over the 68 F water example and the major point of this article.
Many sales engineers, pump technicians and operators will work for years in the pump application world and will have no pump suction side issues with NPSHa until that first time they encounter an application involving hot liquids (higher vapor pressures), where the previous “forgiving adequacy” of 34 feet NPSHa margin was just “mysteriously stolen” from them by the thief that is vapor pressure. A similar scenario plays out when people who have always worked with applications involving flooded suctions are instead confronted by a project with a lift or a vacuum on the suction side.
To continue the full calculation for this example, the head due to static height (hst) is positive because it is a flooded suction above the pump centerline.
When the water temperature was 68 F, the NPSHa was 40 feet. Now that the water is 212 F, the NPSHa has dropped to 6.8 feet—a significant difference of 33.2 feet.
The significant difference for the current example is that the vapor pressure will be higher because the temperature is higher. The vapor pressure for 68 F water is 0.783 feet. (To obtain that value convert 0.33889 psia to head by multiplying by 2.31 and dividing by specific gravity, which was 1.0.) But now the vapor pressure for 212 F water is 35 feet. See Equation 3. This is a significant difference of almost 34 feet over the 68 F water example and the major point of this article.
Many sales engineers, pump technicians and operators will work for years in the pump application world and will have no pump suction side issues with NPSHa until that first time they encounter an application involving hot liquids (higher vapor pressures), where the previous “forgiving adequacy” of 34 feet NPSHa margin was just “mysteriously stolen” from them by the thief that is vapor pressure. A similar scenario plays out when people who have always worked with applications involving flooded suctions are instead confronted by a project with a lift or a vacuum on the suction side.
To continue the full calculation for this example, the head due to static height (hst) is positive because it is a flooded suction above the pump centerline.
When the water temperature was 68 F, the NPSHa was 40 feet. Now that the water is 212 F, the NPSHa has dropped to 6.8 feet—a significant difference of 33.2 feet.