
It is said that people find comfort in the familiar. This is probably why many engineers shy away from the ominous task of understanding a fluid that does not behave like a more familiar fluid, such as water. It is difficult to think of a more common, or familiar, fluid than water. Water also happens to behave as a Newtonian fluid, meaning the viscosity never changes. But what exactly is viscosity, and what happens when a fluid’s viscosity behaves in an unfamiliar way?
Viscosity
Viscosity is a characteristic of a fluid that describes the fluid’s resistance to deform or flow. A synonymous term to describe this behavior is fluid thickness. A fluid with a high viscosity will appear thick and resist flowing, whereas a fluid with a low viscosity will flow easily and quickly. Viscosity is always a positive value, although a superfluid can approach zero viscosity. Some fluids with high viscosity can even appear to be solid. A classic example of a fluid with a high viscosity is molasses because of how slowly it moves.
Fluid hydraulics is concerned with how fluids flow through pipes, so a fluid’s flow resistance is a helpful behavior to understand when designing pipelines and networks or even sizing pumps. Hydraulic modeling software is often used to size pumps and calculate flow and pressure of a fluid as it travels through a pipe.
Additionally, it is important to distinguish viscosity from density. Density is the amount of mass per volume of a fluid and is relatively constant for liquids. Imagine a person with two 1-gallon jugs of different liquids. The liquids could have the same density—that is, the same amount of mass in each jug—but one liquid has a high viscosity and the other a low viscosity. Each gallon will have the same amount of mass because the density is the same, but when the person begins pouring the liquid out, the one with the lower viscosity will pour out faster than the other. The density is unrelated to the viscosity.
The units to describe viscosity are mass per time-length. In English units, lbm/hr-ft (pound-mass per hour-foot) is often used and in metric, Pascal-second (Pa-s) is used. For simplicity, centipoise (cP) is often used instead of Pa-sec, where 1 Pa-sec is equal to 1,000 cP. Also, for reference, water at a temperature of 68 F (20 C) has a viscosity of 1 cP (2.42 lbm/hr-ft).
Viscosity is an important fluid characteristic to consider when designing and analyzing pumps and pipes. A fluid with a high viscosity will require a larger pressure differential for it to flow, which impacts pump performance, energy efficiency and friction losses. Fortunately, this is straightforward to hand-calculate and easy to model with flow analysis software when viscosity is constant, as is the case for Newtonian fluids.
Viscosity for Newtonian Fluids
A Newtonian fluid has a fixed fluid viscosity. Regardless of the velocity of the fluid, the viscosity never changes. This is helpful when calculating pressure losses through pipes because the Darcy or Fanning friction factors can be used.
The Darcy friction factor is a function of Reynold’s number for laminar flow and absolute roughness, pipe diameter and Reynold’s number for turbulent flow. The Darcy friction factor, along with pipe length, diameter, density and velocity squared, is used to calculate the pressure loss through a pipe. This calculation is relatively straightforward and computationally simple as long as the ideal Newtonian assumption is applied. Hydraulic modeling software can perform these calculations quickly and with high accuracy. Once the assumptions of constant viscosity at varying fluid velocities start breakdown, complex viscosity calculation methods are needed because the fluid is now considered non-Newtonian.
Viscosity for Non-Newtonian Fluids
While a Newtonian fluid’s viscosity is fixed and independent of fluid velocity, a non-Newtonian fluid’s viscosity is variable and dependent on fluid velocity. For example, a non-Newtonian fluid flowing through a pipe may have a low viscosity, akin to water. As the flow rate increases, the velocity of the fluid in the pipe increases. In turn, the fluid viscosity may decrease because of the velocity increase. Viscosity can change at different velocities because, by definition of a non-Newtonian fluid, viscosity is dependent on the instantaneous shear rate of the fluid.
To visualize shear rate, imagine a deck of cards sitting on a table. With your hand, you apply a force to the top of the deck, parallel to the table. The first card will begin to slide, and the card just below it will slide as well but not quite as far. Even though the force is only applied to the top card, each card below slides slightly in the direction of the force. Similarly with a fluid against a pipe wall, as the fluid moves through the pipe, the pipe wall is exerting a friction force parallel to the flow direction. The viscosity of a non-Newtonian fluid will change as the shear rate changes. For example, as the shear rate increases, the viscosity of the fluid could increase making it appear thicker and induce a larger pressure drop through that pipe. The opposite could also occur. As shear rate increases, the fluid viscosity decreases and it flows more easily. The fluid could also have a yield stress associated with it. This means that a small amount of force applied to the fluid will not deform the fluid but once that force is large enough, the fluid will deform and flow.
Modeling and calculating the pressure loss of non-Newtonian fluids is a complex task. To quantitatively capture the non-Newtonian characteristics of a fluid, there is myriad test equipment and theoretical models with names unique to an industry or application. Each non-Newtonian model could use different equations to calculate the frictional losses in the system.
This is where hydraulic modeling software can improve the speed and accuracy of hydraulic calculations for non-Newtonian fluids. With the data to describe the viscosity characteristics of a fluid, the viscosity can quickly be calculated as velocity, and thus viscosity varies through pumps, pipes, tees, valves and bends. The results can also be compared using different fluid models available in the software without redoing time-consuming hand calculations. Although numerous models exist to quantitatively capture the behavior of non-Newtonian fluids, the Power Law model and Bingham plastic model are among the two most commonly used in hydraulic modeling software.
Power Law Model
The Power Law for non-Newtonian fluids is a common viscosity model used in hydraulic analysis. This model states that the shear stress required to shear a fluid at a given rate can be described in Equation 1.
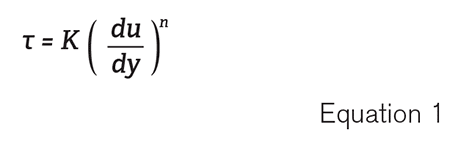
Here, τ is the shear stress, du/dy is the shear rate (or velocity gradient), and K and n are the Power Law constants that are empirically determined.
The Power Law model defines η, the apparent viscosity of the fluid in Equation 2. In the Power Law model, a value of n = 1 corresponds to a Newtonian fluid, while 0 < n < 1 is a shear thinning (pseudoplastic) fluid and n > 1 represents a shear thickening (dilatant) fluid.
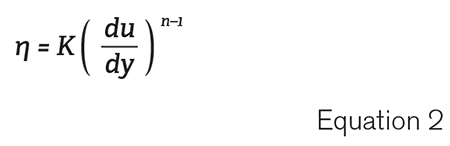
Using rheological data to obtain values for K and n, the viscosity can be calculated at any shear rate. Then Moody friction factors are calculated to ultimately calculate pressure loss through the pipe.
Bingham Plastic Model
The Bingham plastic model for non-Newtonian fluids is another common viscosity model used in hydraulic analysis. This model states that the shear rate resulting from a given shear stress applied to the fluid can be described with Equation 3. Where du/dy is the shear rate (or velocity gradient), τ is the applied shear stress, Sy is the yield stress, and Rc is the plastic viscosity or coefficient of rigidity.
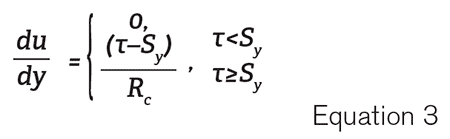
The Bingham plastic model describes η, the apparent viscosity of the fluid in Equation 4.
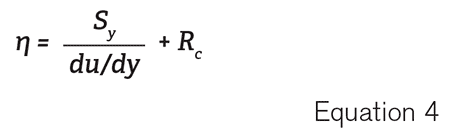
In the Bingham plastic model, a value for Sy of 0 would result in a Newtonian fluid. Some fluids may see Bingham pseudoplastic behavior, where shear stress and shear rate do not have a linear relationship (often modeled with the Herschel-Bulkley viscosity model).
Correctly Sizing Pumps
Fluid viscosity characteristics are crucial to understand for pumps. The rotating impellers in a pump are applying a shear rate to the fluid. For a Newtonian fluid, the viscosity does not change based on the shear rate, so regardless of the pump speed, the viscosity remains the same. For a non-Newtonian fluid, the speed of the pump directly affects the viscosity of the fluid being pumped. For most non-Newtonian fluids, the viscosity will be high before it starts flowing, but once it starts moving, its viscosity decreases, reducing the pump power required. Imagine ketchup: It is thick at first in the bottle but, once it starts moving, pours easily.
The problem with pumps is often a pump is sized based on the low viscosity of the fluid when it is flowing. The high viscosity of the stationary fluid is neglected, leading to pumps that cannot start because the fluid is too thick at first. The pump is functionally undersized when the full picture of viscosity is understood. A low viscosity can also have adverse effects on a pump due to slip and low pump output. Thus, knowing the minimum and maximum viscosity, at what shear rate these viscosities occur, and how the pump will perform at both ends of the spectrum is important.
Hydraulic modeling software can assist with transient calculations for non-Newtonian fluids for pump startups and trips. This can help an engineer in sizing a pump for an unfamiliar fluid. As for systems, recirculation loops and variable frequency drives can help overcome common issues getting a non-Newtonian fluid to flow initially. These alterations can be included in the hydraulic model so a user knows the effectiveness of the changes.
Viscosity is an important fluid characteristic to understand when designing systems and sizing pumps. Understanding how a fluid’s viscosity can change at various shear rates can help users avoid installing an incorrectly sized pump. Using hydraulic modeling software can save time and money and improve accuracy.

