The equivalent suction lift is equal to the difference between the “vacuum effect” and the net submergence.
Summit Pump, Inc.
11/19/2018
In the first four parts of this five-part series, we covered the calculation of NPSHa for a flooded suction, a lift condition, a hot water flooded suction and a pressurized hot water flooded example. In this fifth and final working example, we will investigate what happens to NPSHa when the system is under vacuum.
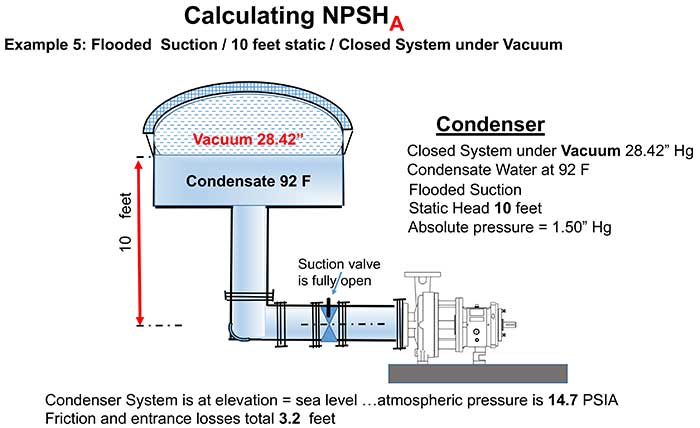 Image 1. Flooded suction/10 feet static/closed system under vacuum (Image courtesy of the author)
Image 1. Flooded suction/10 feet static/closed system under vacuum (Image courtesy of the author)
Vacuum
The concept of vacuum is frequently misunderstood and is a source of confusion to many in the pump world. In general, people that manufacture, sell, maintain and operate vacuum pumps and other related vacuum equipment know the terms, units and principles very well, but the rest of us are often confused and dismayed by the subject. Nomenclature in the world of vacuum applications can be confusing and is often counterintuitive; for example, the term “high vacuum” simply implies low pressure. The higher the vacuum, the lower the remaining pressure, and vice versa. What if I told you that vacuum is pressure? Most people would surely dismiss that statement as silly, but please think about it. In a vacuum, there remains an amount of pressure that is below atmospheric pressure, but is also above absolute zero. Even in a container at “middle to high vacuum” there is some pressure remaining. The application example for this article is a steam condenser. Condensers operate in a vacuum by design because this approach maximizes efficiency for the steam system. If you are applying pumps in commercial or industrial applications, you will eventually encounter a situation where the liquid on the suction side of the pump is under vacuum. Condensers are not the only applications concerned with vacuum. The pressure in the suction line of a centrifugal pump operating in a lift application will most often be in a vacuum—that is, at a pressure less than atmospheric. To be clear, when we state a pressure, we should add the mode to differentiate the pressure measurement we are referencing. That is, we should state with the units and measurement quantity the correct mode; either vacuum, atmospheric, gauge or absolute. For this article, we will refer to the area of vacuum as that pressure range (mode) below atmospheric pressure and above zero pressure absolute. Note that atmospheric pressure changes with the weather (barometric pressure) and the elevation above or below sea level. Image 1. Flooded suction/10 feet static/closed system under vacuum (Image courtesy of the author)
Image 1. Flooded suction/10 feet static/closed system under vacuum (Image courtesy of the author)
