
If you have read news about pumps and motors in the last 10 years, you know there is increasing pressure to create more efficient pumps. The pump energy saving initiatives are similar to what has transpired over the last 15 years with alternating current (AC) electric motor design.
Starting in 2011, and coming to fruition in 2020, the United States Department of Energy (DOE) placed requirements (regulations) on centrifugal water pumps to meet minimum efficiency levels. Some of this work started in the 1990s, but the regulations (“Energy Conservation Standards for Pumps”) came years later.
The Hydraulic Institute (HI) has initiated numerous programs, ranging from public awareness to in-depth training and management guides. As their website states, “HI has taken a leading role in representing the pump industry in negotiating fair and appropriate regulations designed to achieve energy savings goals.”
I was recently contacted by an engineering college for my input on designing more efficient pumps. I eagerly prepared for the meeting, but the project was canceled due to the COVID-19 pandemic. Afterwards, like a really bad marketing jingle, I couldn’t get the topic of pump efficiency out of my brain. Ideas for improving efficiency replayed in my head in a pedantic voice burned into my cortex by my paternal grandmother: “Easier said than done,” and “You can’t get something for nothing,” played in a continuous loop.
For the record, I think higher efficiency is both a commendable goal and a high priority in my work. In conflict with this goal, my personal opinion is that if you don’t design the associated pumping system correctly and operate the pump properly, it doesn’t matter if the pump is efficient or not. The pump and the system must work together—one needs the other.
Efficiency
The basic definition of efficiency is a simple formula. Efficiency is the ratio of output divided by the input and then multiplied by 100 to express it as a percentage.
If your vehicle has a gasoline engine, it is about 20 percent efficient; if the engine is diesel, it may improve to 30 percent or more. The efficiency of a coal-fired or nuclear power plant can approach 38 percent. Gas-fired power plants with a combined cycle can approach 60 percent. Modern AC induction motors have recently approached 99 percent efficiency, but most often are 91 percent to 95 percent at near full load conditions.
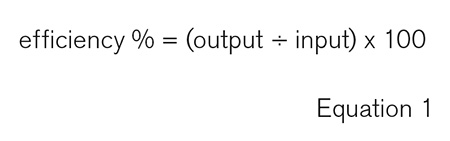
Centrifugal pumps can approach 94 percent efficiency, but typical efficiencies are 55 percent for small pumps and 70 percent for large pumps. The amount of electrical energy used by the pumps in an average industrial facility will vary by plant type. A typical pulp and paper mill will use 30 percent of their energy usage to drive pumps. A chemical plant may use 27 percent and a petroleum refinery may use 60 percent. Over a short time, the cost of the energy to drive the pump will exceed the initial purchasing and installation costs. Over a 20-year period, it is common for the energy costs of a typical 100-horsepower pump to exceed 20 times the initial cost of the pump, including installation.
Pump Efficiency
Pump efficiency is the “water horsepower” divided by the “brake horsepower” and multiplied by 100 to present it as a percentage (see formulas in Image 1).
Water horsepower is a system design tool and is the power that the pump would require to accomplish the hydraulic conditions if it was 100 percent efficient. The efficiency of the pump is not a factor in the water horsepower equation. Water horsepower defines the lowest boundary for the power requirements. Or, think of it as the minimum power required to move the fluid (water). This is handy information to have in the early stages of a plant design. Note that the specific gravity should be used when doing this calculation.
Brake horsepower (BHP) is the shaft horsepower the pump requires to meet the load. Brake horsepower takes pump efficiency into account, but not the motor efficiency. This data is used to size the driver. Pump input horsepower and efficiency can be calculated from the basic BHP formula, but when preparing the performance curves, the manufacturer will measure the speed and torque of the motor shaft input to the pump. The pump efficiency is a simple calculation once you have the speed and torque data.
Wire-to-water efficiency is the amount of energy that is imparted to the pumped fluid (water) divided by the energy that was introduced by the electrical system—or the work completed divided by the work applied. When using fractions or decimals, we can multiply in lieu of dividing, and so the wire-to-water efficiency is the pump efficiency multiplied by the motor efficiency. This information allows us to properly size the electrical service to the motor. (Wire-to-water efficiency is referred to as wire-to-liquid efficiency if the fluid is not water.)
For example, a motor that is 90 percent efficient that is driving a 70 percent efficient pump produces a real efficiency of 63 percent (0.90 x 0.70 = 0.63 or 63 percent efficient). Note: it is not the average efficiency of the two factors, which is a common mistake. Wire-to-water efficiency becomes a major factor and is an important tool when calculating the power cost for pumping a specific amount of liquid.
Why Isn’t the Pump More Efficient?
Some factors preventing the pump from obtaining higher efficiency are noise, vibration, recirculation and heat. Other impediments to pump efficiency include:
Mechanical efficiency factors, which are mostly frictional losses from bearings, packing, mechanical seals, impeller/rotor imbalance, couplings and driver misalignment.
Volumetric efficiency is the sum of the losses from leakage across wear rings, impeller clearance to casing, interstage bushings, balance drums, warm-up/bypass lines and internal flow back to the stuffing box/lantern ring.
Hydraulic efficiency factors are the largest hindrance. This is the sum of all the fluid friction losses in the pump, including disc friction and hydraulic shock losses. Shock losses are due to the rapid acceleration and deceleration of the fluid, which are greater at low flow rates and are a function of impeller geometry. The shock factor is why high specific speed impellers will typically be more efficient.

Part 2 of this column will focus on making the pump more efficient.
Read more Common Pumping Mistakes articles here.

