Centrifugal pumps have many advantages compared with positive displacement pumps. They have the ability to run all over the curve. Open the valve to increase the flow, and close it to decrease the flow. This seems convenient and simple. However, this convenience can cause problems for end users. There are many indications that they should not use a valve for flow control—or at least not to extremes. Staying close to the best efficiency point (BEP) is ideal to save energy and to avoid having a problem pump. Pump manufacturers note a minimum continuous stable flow (MCSF) line on their pump performance curves. A centrifugal pump can operate below (to the left of) the MCSF, but it is not recommended. Hydraulic instabilities can become dramatic and cause pressure pulsations, vibrations, axial shuttling of the rotor and failures. The ideal MCSF depends on many factors—such as design type and energy levels. A good rule of thumb is to avoid operating a pump below 50 percent of the BEP flow. Some specifications—such as American Petroleum Institute 610—would limit the MCSF even more. Operating a pump below the MCSF, hydraulically stable, can cause damage. Operating below the minimum continuous thermal flow (MCTF), thermally stable, can be disastrous. The MCTF is much lower than the MCSF. When a discharge valve is closed or nearly closed, an operator can literally boil the fluid within the pump. The energy that the impeller generates into the fluid trapped within the casing by the closed valve transfers into heat (see Equation 1). Equation 1: Q = cm∆T Where: Q = heat added c = specific heat m = mass ∆T = the change in temperature
 Image 1. A single-stage, overhung impeller centrifugal pump, driven by a 150-horsepower motor at 1,800 rpm, with 12-inch suction and discharge nozzles
Image 1. A single-stage, overhung impeller centrifugal pump, driven by a 150-horsepower motor at 1,800 rpm, with 12-inch suction and discharge nozzlesCase Study
If the trapped fluid is air, the pump can become hotter much faster. As an example, let’s take a single-stage, overhung impeller centrifugal pump, driven by a 150-horsepower motor at 1,800 rpm, with 12-inch suction and discharge nozzles (see Image 1of the partially disassembled pump to show the impeller and casing). A 12-inch pipe, about 10 feet long, is between the pump suction flange and the supply tank, and a discharge valve is closed while the pump is operating. The motor power during the shut-valve condition depends on the design and type of a pump. For this article, assume it is less than half the power at the BEP, about 60 horsepower (40 kilowatts), which is reasonable for many pumps. This power has nowhere to go and must dissipate into the fluid inside the pump casing. Eventually, through thermal convection, it heats the water in the suction pipe and in the supply tank. If thermal convection is quick, it will take a long time to heat the water, as the mass of water in suction pipe and the tank will keep the temperature rise to a minimum. However, the internal hydraulics of the impeller-to-volute interaction could mean that the main portion of fluid affected by the rapid heating is only a portion of fluid trapped between the impeller outside diameter (OD) and the casing outside boundary away from the impeller. If this is the case, the volume of fluid subjected to heating is much smaller, and it will heat quickly. If the fluid is water, the water mainly affected thermally is within the space outside the 14-inch OD impeller vanes, which was roughly 6 inches wide with about a 2-inch gap from the OD to the casing wall (see Equation 2). Equation 2: 3.14 x (14/12) x (6/12) x (2/12) = 0.5 cubic feet (ft3) of trapped volume If the above formula (for water the specific heat (Cp) = 4 kilojoules (kJ)/kilogram (kg) C for the mass of the trapped water: 0.5 ft3 x 62.4 lb/ft3 = 31 lb = 14 kg Each second, 40 kW x 1 sec or 40 kJ are transferred into the trapped volume of water. Substituting the values into Equation 1 results in: 40 = 4 x 14 x ∆T ∆T = 0.7 C or about 1 F In one minute, the temperature will increase 1 x 60 = 60 C. If the pump is on a lift, and it started unprimed, the fluid inside the volute is air. It has the same volume and will become hot faster because of air’s lower value of specific heat (Cp = 1.0 kJ/kg C). The energy entering the air is significantly less than it was for the water (by a multiple of specific gravity), but the mass is lower, too: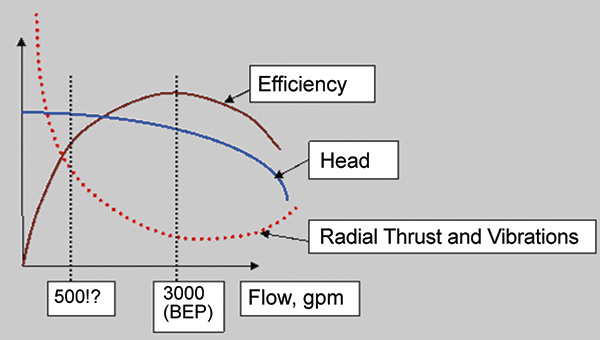 Figure 1. Pump performance curves and operating points. Source: www.pump-magazine.com/pump_magazine/pump_articles/article_17/article_17.htm
Figure 1. Pump performance curves and operating points. Source: www.pump-magazine.com/pump_magazine/pump_articles/article_17/article_17.htm- A system with an insulated pipe
- A system with a pipe with the insulation removed

