Parallel operation is a setup in which two or more pumps take suction from the same suction header and deliver liquids into the same discharge header. In theory, if the two pumps and piping are identical in design, they should pump at approximately the same flow rate. However, differences in piping, pump performance and internal wear often lead to flow discrepancies in pumps operating in parallel. Indiscriminate parallel operation of centrifugal pumps may lead to significant flow imbalances that can result in pump vibration, pulsations, overheating and failure. Pump users should always confirm that pumps are similar in performance capabilities before operating them in parallel. Individual flow meters can help ensure that pumps are operating at a safe flow when in a parallel arrangement. A total flow meter for a group of pumps is more common. In one scenario, two centrifugal pumps—nine-stage, 125-horsepower (hp) vertical turbine pumps—are installed side by side. They transfer pipeline liquids collected upstream of a compressor station into another pipeline. These pumps were never intended to operate in parallel. Normally, one of the pumps can handle all liquids reaching the station.
 Image 1. One of two nine-stage, 125-hp vertical turbine pumps that are rated for 350 gallons per minute (gpm) and 3,550 revolutions per minute (rpm) (Images and graphics courtesy of Enterprise Products)
Image 1. One of two nine-stage, 125-hp vertical turbine pumps that are rated for 350 gallons per minute (gpm) and 3,550 revolutions per minute (rpm) (Images and graphics courtesy of Enterprise Products) The team began their analysis using Equation 1, which was developed to approximate the efficiency of a centrifugal pump in the field. This equation can determine a motor-driven centrifugal pump’s efficiency under process conditions. This equation does not require the fluid’s specific gravity, which is useful when the specific gravity of the pumped liquid is not known.
The team began their analysis using Equation 1, which was developed to approximate the efficiency of a centrifugal pump in the field. This equation can determine a motor-driven centrifugal pump’s efficiency under process conditions. This equation does not require the fluid’s specific gravity, which is useful when the specific gravity of the pumped liquid is not known.
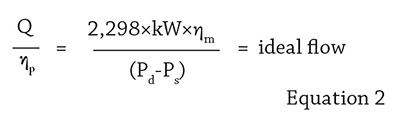
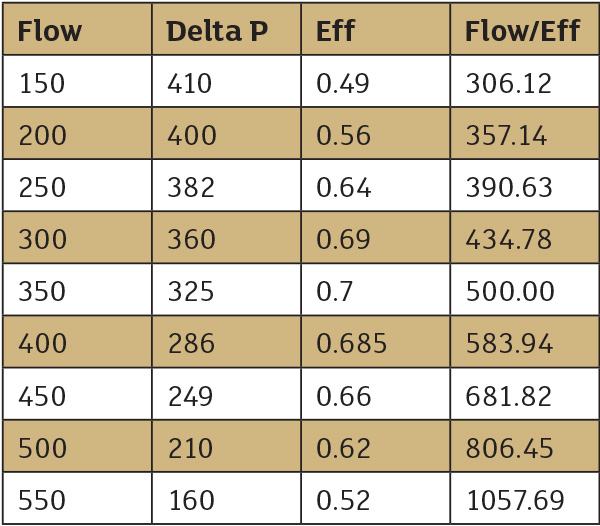 Table 1. Pump performance data
Table 1. Pump performance data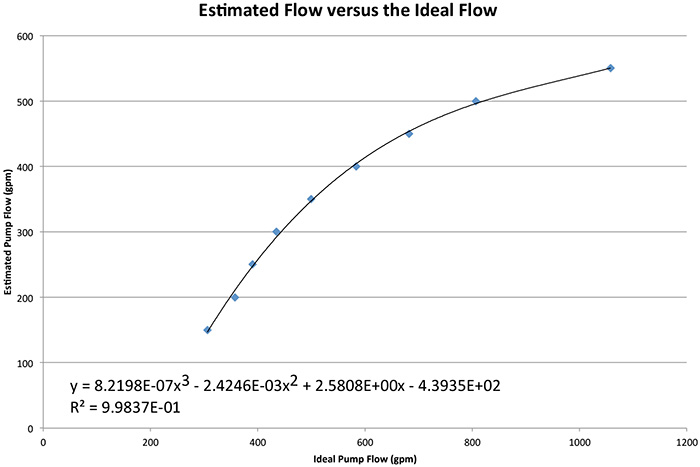 Figure 1. Plot of ideal versus estimated pump with best fit equation
Figure 1. Plot of ideal versus estimated pump with best fit equationResults in the Field
Two new power meters were installed in the field, and their outputs were tied into a local PLC, along with pump suction and discharge pressures. The PLC was programmed to perform all calculations for an estimated flow rate.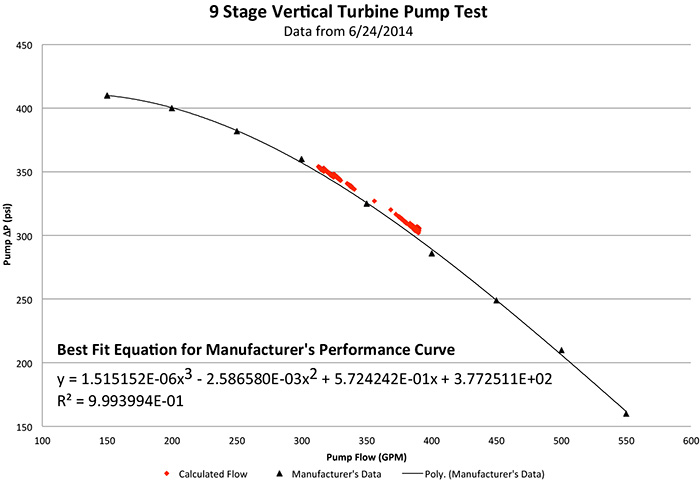 Figure 2. Comparison of manufacturer’s predicted performance versus the actual field data
Figure 2. Comparison of manufacturer’s predicted performance versus the actual field data
