The Thirteenth in a Series
If a centrifugal pump is started with the discharge valve open too far and with a low discharge pressure, the liquid in the suction line may accelerate at a rate that causes the suction pressure to drop below vapor pressure. In other words, you can cause cavitation by allowing the pumpage to accelerate too rapidly in the suction line.
If the pump's capacity is controlled by a quick opening valve on the discharge side (such as seen in steel mill descaling systems), the pump may be provided with insufficient NPSH when the pumpage is accelerating to the rated capacity.
The equation for calculating the head drop due to the acceleration (assuming uniform acceleration) may be reduced to the following:
![]()
Where:
ha = Head required to accelerate the liquid in the suction line, feet or meters
L = Total length of the suction line, feet or meters
V2 = The final velocity of pumpage, feet/sec or meters/sec
V1 = The initial velocity of pumpage, feet/sec or meters/sec
g = Acceleration of gravity (32.2 ft/s2 or 9.8 m/s2)
t = Time increment that pumpage accelerates from V1 to V2, seconds
Acceleration Head for Reciprocating Pumps
Pulsing Flow Requires More NPSH
The flow in the suction and discharge piping of a reciprocating pump is not constant. The pumpage must accelerate and decelerate a number of times for each revolution of the crankshaft. Because the liquid has mass, and therefore inertia, energy is required to produce the acceleration. This energy is returned to the system upon deceleration, so there is no loss. However, sufficient NPSH must be provided on the suction side of the pump to accelerate the liquid to prevent cavitation in the suction pipe and/or pumping chambers.
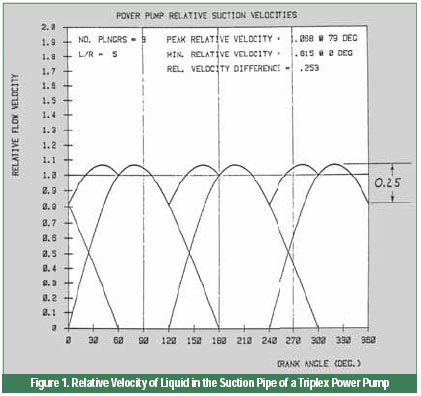
Figure 1 plots the ideal relative fluid velocity in the suction pipe for a typical triplex power pump as a function of the rotative angle of the crankshaft. (To achieve this ideal velocity profile, the pumpage must be incompressible, and the pump valves must open and close at the beginning and end of the plunger stroke, which is often not the case.) Acceleration may be more clearly visualized if we change the scales on this curve. If we change the abscissa from degrees of rotation to time (which is done by dividing by 360 and revolutions per second), and change the ordinate to pipe velocity rather than relative velocity (by multiplying by average pipe velocity), we have a plot of velocity versus time in the suction pipe.
Since acceleration is the rate of change of velocity with respect to time (dv/dt), we can determine acceleration simply by measuring the slope of the velocity curves. We see that a triplex pump produces maximum acceleration at 0 deg, 120 deg and 240 deg of crankshaft rotation.
The Acceleration Head Equation
We can calculate the mass of liquid in the suction line, and its acceleration. Then using Newton's second law (F = ma) we can calculate the force required to accelerate that mass. We can then convert this to pressure by dividing by the cross-sectional area of the pipe. Fortunately this has already been done, and appears in a number of documents. The first known appearance of the equation shown below was in a section of Marks' Handbook (5) by Elliott Wright. The author accepted and promoted it, and it subsequently appeared in Hydraulic Institute standards (2). Those documents provide the following equation:
![]()
Where:
ha = Acceleration head, feet
L = Actual length of suction line, feet (not equivalent length)
V = Average liquid velocity in suction line, feet/second
N = Speed of pump crankshaft, revolutions/minute
C = Constant depending on pump type
= 0.400 for single‑acting simplex
= 0.200 for single‑acting duplex
= 0.115 for double‑acting duplex
= 0.066 for triplex
= 0.040 for quintuplex
= 0.028 for septuplex
= 0.022 for nonuplex
g = Gravitational constant = 32.2 feet/sec2
k = Constant depending on fluid compressibility
= 1.4 for non‑compressible liquids such as deaerated water
= 1.5 for most liquids
= 2.5 for compressible liquids such as ethane
Two or More Pumps Running in Parallel
If two or more pumps operate in parallel, with a common suction line, acceleration head is calculated for the common line by assuming that all pumps are synchronized, acting as one large pump. (The capacities of all pumps are added to determine line velocity.)
Dampening the Pulsations
Any characteristic of the suction system that tends to absorb the pulses from the pump will reduce acceleration head. The suction stabilizer, therefore, helps those systems with excessive acceleration head and/or with gas entrained in the liquid. (The most effective suction stabilizer is a flow‑through type that also separates free gas from the liquid. Any excess gas must be vented from the stabilizer, possibly piped back to the vapor space in the suction vessel.)
According to Hydraulic Institute standards (2), a properly selected, installed and maintained dampener will reduce the effective length of the suction line in the above equation to about 10 pipe diameters, i.e., for a 6 in suction pipe, L would be about 60 in (5 ft). This would result in a calculated acceleration head in Problem 1 of only 0.7 psi.
Another effective method of reducing acceleration head on an atmospheric‑pressure suction system is to install a section of soft hose as part of the suction line, adjacent to the pump.
Shortcomings of This Equation
Equation 19‑2 is not sophisticated enough to compensate for such factors as system elasticity and the velocity of a pressure wave in the pumpage (sonic velocity due to liquid elasticity). It is therefore recommended for use only for relatively short, non‑elastic suction lines.
Miller (3) reported that his tests indicated acceleration head to be much less than calculated with the above equation. Some field installations also operate satisfactorily with NPSHA considerably less than this equation indicates as necessary. On the other hand, some installations require NPSH that agrees favorably with this equation.
The reason for these discrepancies is not known, but, in addition to the above, it may be due to gas, such as air, being liberated (or trapped) in the suction line. Any gas entrained in the liquid, or collected at a high point in the suction piping, tends to absorb the pulsations from the pump, and thereby reduces acceleration head.
Some pump operators have reported that suction stabilizers, which were designed to also separate and accumulate gas, have, to their surprise, required periodic venting. If the stabilizer had not been in the suction line (or did not have this separation feature), the pump would have ingested gas, possibly resulting in shock operation, or in the extreme case, causing one or more pumping chambers to become gas bound or vapor locked. Without the stabilizer, the agitation in the suction line would have been greater, and more gas could have been liberated. The pressure shocks caused by gas ingestion can cause failure of pump and system components (1).
The Water Hammer Equation
For a quick closing (or opening) valve, reference 4 provides the equation for water hammer as follows:

![]()
Where:
h = Head increase or decrease
c = Sonic velocity in liquid
V = Change in velocity
g = Acceleration of gravity
This equation provides the maximum head that a quick operating valve can generate. Note that the length of the pipe is absent from the equation, and enters into the evaluation only to the extent that it determines how fast the valve must close (or open) to be considered as quick operating. This equation could therefore be used to calculate a more accurate pump acceleration head if we could accurately determine the change in velocity of the pumpage in the pipe.
Unfortunately, the velocity change is more complex than shown in Figure 1, because it is dependent on the fluid compressibility, the clearance volume in the pumping chamber and the effectiveness of the valve springs in closing the pump valves quickly enough for smooth pump operation. (A weak or broken spring, on either a suction or discharge valve, will cause a significant velocity change.) All these factors are difficult to establish for field installations.
At one time, one pump vendor produced power pumps that, because of unique construction of the fluid end, could not be equipped with springs on the suction valves. A vendor of pulsation dampeners once remarked (without knowing the reason) that that pump brand required twice the discharge dampener of other vendors' pumps. Sound level tests, on a number of brands of power pumps, also revealed that the springless pumps were noisier than equivalent pumps with valve springs. Adequate springs are required on both suction and discharge valves to provide a quiet, smooth running power pump.
References
1. Henshaw, Terry L., Reciprocating Pumps, Van Nostrand Reinhold Co., Inc., 1987.
2. Hydraulic Institute Standards, Hydraulic Institute, 9 Sylvan Way, Suite 360, Parsippany, NJ 07054‑3802.
3. Miller, J. E., "Experimental Investigation of Plunger Pump Suction Conditions", ASME Paper 64‑PET‑14, 1964.
4. Daugherty and Ingersoll, Fluid Mechanics, 5th Edition, McGraw‑Hill Book Co., NY, 1954.
5. Marks' Mechanical Engineers' Handbook, 6th Edition, pg. 14‑6, McGraw‑Hill Book Co, New York, 1958.

