This article is the first of three on centrifugal pump radial thrust. It relates the author’s experience with the use of the traditional equation to calculate radial thrust, subsequent measurements of radial thrust and comparison of the two. Part Two will show a plot of measured radial thrusts imposed on a performance curve and will discuss the pattern revealed. The final part will discuss variations in impeller and casing designs which reduced radial thrust.
Stepanoff Radial Thrust Equation
It was 1958. I was fresh out of college and working in New York City for a major manufacturer of industrial machinery. One of my early assignments was to calculate the shaft deflections of a number of pumps being bid for hydrocarbon processing to a major contractor who required calculations demonstrating that the wear rings would not rub when operated at low capacities. I calculated the radial thrust on the impellers probably using data from Stepanoff [1]. His book offered the following equation for calculating the radial thrust:
Where:
P = radial force, pounds
H = pump head, feet
D2 = impeller diameter [outside diameter—OD], inches
B2 = impeller overall width including shrouds [at the impeller OD], inches
K = a constant that varies with capacity, determined experimentally
Notice that the product D2 x B2 is the projected area of the discharge of the impeller, and H/2.31 is the total differential pressure produced by the pump. The product of pressure x area, therefore, calculates a force. The K factor is intended to adjust that force to the actual radial thrust. The absence of specific gravity in the equation indicates that its use was intended only for cool water. Although the Stepanoff data was precise and detailed, it reported thrust characteristics for only one size pump. In 1959, Agostinelli, et al, reported radial thrust test results for 16 different pumps [2], while continuing the procedure of considering the effective pressure area being the impeller OD x width (D2 x B2).
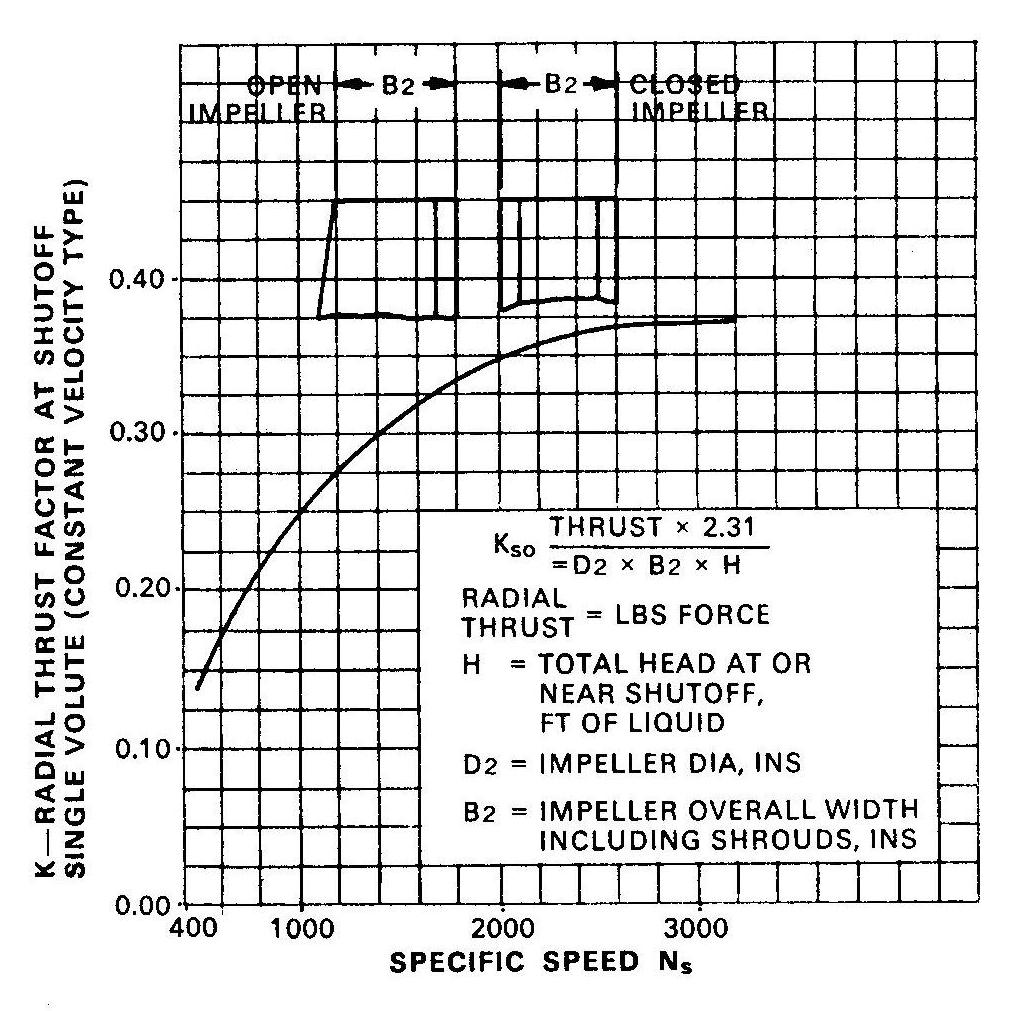 |
|
Figure 1. Radial thrust factor at shutoff for single-volute (constant-velocity) pumps (From Reference 3. Courtesy of the Hydraulic Institute, www.pumps.org, Parsippany, N.J.) |
Hydraulic Institute Curve
In 1969, the Hydraulic Institute (HI) published a curve showing K values at shut-off for single-volute pumps as a function of specific speed [3] (see Figure 1). Although the HI values agreed with Agostinelli [2] in the higher specific speed range (around 3,000), they were almost twice the Agostinelli values in the lower range (around 600). The current HI K value graph, as seen in Figure 2, shows shut-off K values lower than the 1969 graph, and which compare favorably with Agostinelli [2]. The procedure continued to consider the effective area to be D2 x B2.
Actual Radial Thrust of Vertical, In-line Pumps
I learned that, using Equation 1—an accepted, published equation—and K values, produces significantly inaccurate radial thrust values for some pumps. I was asked by a pump manufacturer to determine the actual radial shaft deflection, at the mechanical seal, for a line of vertical, in-line centrifugal pumps, similar to that in Figure 3. The pump shaft was rigidly coupled to the motor shaft so that, when the pump was equipped with a mechanical seal, the motor bearings absorbed both axial and radial thrusts from the pump.
The pumps were equipped with semi-open impellers. The impeller faces were machined at an angle of 20 degrees, resulting in vanes that got wider (an increasing B2 dimension) as the diameter was reduced. Such design is common for impellers in pumps provided to the chemical industry, although uncommon for enclosed impellers and some semi-open impellers. Because the casings were volutes, maximum radial thrust occurred at shut-off (zero gallons per minute).
ANSI Specification B73.2 [4] (partially written by this author) required that the calculated shaft deflection not exceed 2 mills at the gland end of the stuffing box, under maximum radial load. Questions had been raised about a 3 x 2 x 11 single-volute pump, running at 3,500 rpm. To minimize the radial thrust, the impeller exit width (B2), at the 11-inch (maximum) diameter, had been designed at 3/16 inch. The D2 x B2 area (see Figure 4) was, therefore, 2.06 square inches. The shut-off head of 480 feet created a differential pressure, on cool water, of about 208 psi. Specific speed was about 650. Using K = 0.18, from Figure 1, the calculated radial thrust was 77 pounds. With the appropriate motor, the 77 pounds would produce a shaft deflection, just above the mechanical seal, of an acceptable 2 mils. But two competitors reported that measured shaft deflection was considerably higher. It was necessary that we measure the radial shaft deflections.
Our test procedure was similar to that used by Stepanoff [1]. A rigid steel table was fabricated, to which was bolted a motor-coupling-shaft assembly. The shaft position—one-half inch above the location of the seal faces—was measured by a pair of proximity probes, located at right angles. Force gages were used to pull on the end of the shaft (at the location of the impeller) to establish an accurate relation between the radial force at the impeller and shaft deflection, ½ inch above the seal faces. We were able to accurately “calibrate” the motor-coupling-shaft assembly, even including the effect of looseness in the bearings.
When the pump was tested, we learned that the radial thrust imposed on the 11-inch impeller, at shut-off, was 240 pounds, more than three times the value calculated using the information in Figure 1—almost six times the value calculated using K values from the other references. Instead of using just the projected area of the impeller discharge, as illustrated in Figure 4, if we use the total projected area of the impeller, from the 3-inch diameter eye to the 11-inch outside diameter, D2, (see Figure 5) the area changes from the 2.06 calculated above, to 6.56 square inches.
Multiplying that by the 208 psi and by the 0.18 K value from Figure 1, results in a calculated radial thrust of 246 pounds, which is only 2 percent above the measured 240 pounds. The closeness of the agreement indicates that we should consider using this procedure for impellers that get wider as the diameter is reduced (and it may well work for all impellers). More sizes of pumps should be tested to determine if this concept applies to all sizes.
References
1. Stepanoff, A. J., Ingersoll-Rand, Centrifugal and Axial Flow Pumps, John Wiley & Sons, New York, 1948.
2. Agostinelli, A., Nobles, D., and Mockridge, C.R., Worthington, “An Experimental Investigation of Radial Thrust in Centrifugal Pumps,” Paper 59-HYD-2, Transactions of the ASME – Journal of Basic Engineering, American Society of Mechanical Engineers, 1959.
3. Hydraulic Institute Standards For Centrifugal, Rotary & Reciprocating Pumps, twelfth edition, 1969, Hydraulic Institute, New York, N. Y.
4. Specifications for Vertical In-Line Centrifugal Pumps for Chemical Process, ANSI B73.2 – 1975, The American Society of Mechanical Engineers, New York, N.Y.
5. Karassik, Igor J., Worthington, “Centrifugal Pump Construction,” Section 2.2 of the first edition of the Pump Handbook, edited by Karassik, Krutzsch, and Fraser, McGraw-Hill Book Co., New York, 1976.
6. Lobanoff, Val S & Ross, Robert R, United, CENTRIFUGAL PUMPS: Design & Application, Gulf Publishing Co., Houston, 1985.
7. Hydraulic Institute Standards for Centrifugal, Rotary & Reciprocating Pumps, 2009, Hydraulic Institute, Parsippany, N.J.


