Q. For centrifugal pump impellers, what is momentum change, and what is its significance?
A. In single suction impellers the axial force related to the momentum of the incoming fluid should be considered in the pump design, particularly at operating points beyond the best efficiency point (BEP). This only applies to single suction impellers with radial or mixed-flow discharges. The incoming liquid has mass and is traveling at a relatively high velocity. The momentum change as the flow changes direction in the impeller creates an axial force in the same direction as the incoming suction flow that should be taken into account in overall axial thrust calculation.
It is most significant in vertical turbine pumps that are designed with limited or no bearing capacity to resist axial thrust in the upward direction. In some designs, the axial movement of the rotor is sufficient to cause contact between the impeller shroud and the diffuser wall.
The magnitude of the axial thrust due to momentum change can be determined with the following equation:
Q. I sometimes see reference to NEMA motor design B. What does this refer to? Are there other design types?
A. Motors can be made in any of the following designs, each of which has a different torque characteristic. See figure C1.3.1.3.2b below.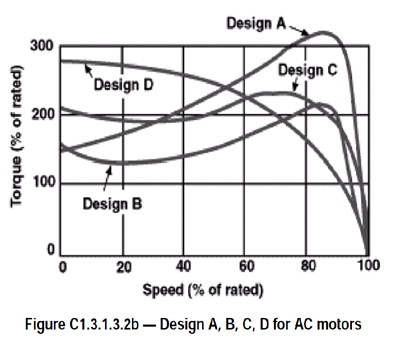
Design A has a normal starting torque (typically 150 to 170 percent of rated) and relatively high starting current. Breakdown torque is the highest of all NEMA types. It can handle heavy overloads for a short duration. Slip is ≤5 percent. A typical application is powering injection-molding machines.
Design B is the most common type of AC induction motor sold. It has a normal starting torque, similar to design A, but offers a low starting current. Locked rotor torque is good enough to start many loads encountered in industrial applications. Slip is ≤ 5 percent. The motor efficiency and full-load power factor are comparatively high, contributing to the popularity of the design. Typical applications include pumps, fans and machine tools.
Design C has a high starting torque (greater than the previous two designs, for example 200 percent), and is useful for driving heavy breakaway loads. These motors are intended for operation near full speed without great overloads. The starting current is low. Slip is ≤ 5 percent.
Design D has a high starting torque (highest of all the NEMA motor types). The starting current and full-load speed are low. High slip values (5 to 13 percent) make this motor suitable for applications with changing loads and attendant sharp changes in motor speed, such as in machinery with flywheel energy storage. Speed regulation is poor, making the D design suitable for punch presses, cranes, elevators and oil well pumps. Several design subclasses cover the rather wide slip range. This motor type is usually considered a special order item.
Q. What is acceleration head for a reciprocating power pump, and how is it calculated?
A. Total suction lift is the difference between the absolute operating inlet pressure at the centerline of the pump inlet port and atmospheric pressure. It is also the sum of the suction system frictional losses and the static suction lift. Total suction lift, as defined above, represents the average, without reference to the fluctuation above and below this average due to the inertia effect of the liquid mass in the suction line. This pressure fluctuation or acceleration pressure must be taken into account if the pump is to fill properly without separation and pounding or vibration of the suction line.
With the slider-crank driver of a power pump, maximum plunger acceleration occurs at the start or the end of each individual stroke, and this is reflected in a similar discontinuity in the cyclical pattern of the combined flow curve corresponding to each piston or plunger and crank arrangement. The pressure required to accelerate the liquid column is a function of the length of the suction line, the average velocity in this line, the rotative speed, the type of pump and the relative elasticity of the liquid and the pipe. It may be calculated as follows: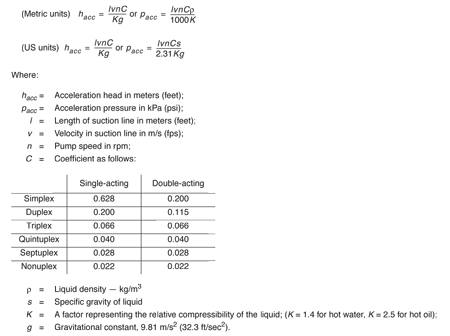
Note: This calculation provides a conservative estimate of acceleration head losses for pipe lengths up to 15 meters (50 feet). For additional details on this subject, please see ANSI/HI 6.1-6.5, American National Standard for Reciprocating Power Pumps for Nomenclature, Definitions, Application, and Operation.

