Vlaming (3) concluded that it was not reasonable to eliminate all cavitation in an impeller, and settled on 40,000 hours (five years) as a reasonable life of an impeller. His NPSH recommendations for obtaining 40,000 hours with a properly designed, stainless steel impeller pumping cool water can be condensed to the following equation:
NPSHR40K = 1.2 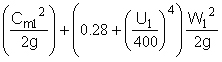 (13‑8)
(13‑8)
This equation applies only to the capacity (flow rate), which results in non‑prerotating, shockless entry of the pumpage into the impeller vanes.* That capacity is normally about 20 percent higher than the best efficiency capacity, but can be even higher (1).
Equation 13‑8 can be rewritten, in terms of U1 and β1, as follows:
NPSHR40K = 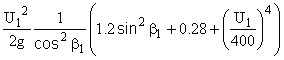 (13‑9)
(13‑9)
Converting to suction specific speed results in:
S40K = 8150 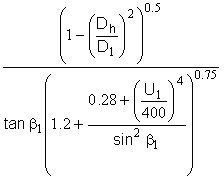 (13-10)
(13-10)
Equation 13‑10 is plotted in Figure 1, for Dh = 0 and β1 = 17˚(which is the angle for which S40K is maximum). Vlaming stated that his experience did not exceed a U1 of 220 ft/sec, so the S40K values above 220 ft/sec must be recognized as extrapolated.
Conditions that apply to the 40,000 hour curve are:
1. Cool water
2. Stainless steel impeller
3. Impeller vanes properly twisted and tapered. (For plain vanes, S is lower.)
4. β1 = 17˚
5. No‑prerotation, shockless‑entry capacity
6. No hub, shaft or fastener blocking part of the eye. If the eye is partially blocked by a hub, shaft or fastener, multiply S from the figure by (1-(Dh/D1) 2)0.5
This author's work (9), supported by Yedidiah (5), demonstrated that, based on the 3 percent head drop, the approximate suction specific speed, calculated at Qbep, varies with U1 as follows:
S3 = C U1 0.375 (13‑11)
Gongwer's work (10) allowed this author to determine that S3 reaches its peak value when β1 = 10˚. With β1 = 10˚, Equation 13‑11 becomes:
S3 = 2520 U1 0.375 (13‑12)
Equation 13‑12 is also plotted in Figure 1.
Note that the 3 percent head drop curve is based on Qbep and β1 = 10˚, and the 40,000 hour curve is based on Qnp and β1 = 17˚, so the two curves are not directly comparable. However, the figure does provide a general comparison, and it emphasizes the diversion of S values as U1 increases. Any S value selected from the top curve could result in a problematic pump.
* Vlaming provided a set of curves for estimating NPSHR40K for capacities above and below the non-prerotating shockless capacity, which showed that the NPSHR40K is higher at all capacities other than shockless.

Figure 1
Nomenclature
SYMBOL |
DEFINITION |
UNITS |
EQUATION |
| β1 |
The angle of the inlet edge of the impeller vane, at the point where the vane joins the front shroud, measured in a plane tangent to the shroud surface. |
Degrees | |
| Ae |
Eye area. The net flow area just upstream of the impeller vanes. |
Square Inches |
(π/4)( D12‑ Dh 2) |
| BEP |
Best efficiency point. The capacity (flow rate) at which pump efficiency is a maximum. |
||
| Cm1 |
The meridional component of the velocity of the liquid just upstream of the impeller vanes. |
ft/sec | 0.321 Q/Ae |
| D1 |
Diameter of the circle prescribed by the inlet edge of the impeller vane, at the point where the vane joins the front shroud (Typically equal to the diameter of the impeller eye) |
Inches | |
| Dh |
Diameter of impeller hub, shaft or fastener, in the plane defined by the outer points of the leading edges of the impeller vanes. |
Inches | |
| g | Acceleration of gravity | 32.2 ft.sec2 | |
| N | Rotative speed of impeller | rev/min (rpm) | |
| NPSH3 |
The NPSH available to the pump coincident with a 3 percent pump head loss |
Feet | |
| NPSH40k |
As defined by Vlaming (3), the NPSH required by a pump, with a stainless steel impeller, pumping cool water, to obtain an impeller life of 40,000 hours |
Feet | |
| P1 |
The meridional velocity through the impeller eye required to obtain a right triangle with U1 and W1 |
ft/sec | U1 tan β1 |
| Qe |
Capacity (flow rate) through each impeller eye |
GPM | |
| Qbep |
Capacity (flow rate) of the pump when pump efficiency is at its peak |
GPM | |
| Qnp |
Capacity (flow rate) through each impeller eye, when Cm1 = P1 (no prerotation, shockless entry) |
GPM | 3.12 P1Ae |
| S3 |
Suction specific speed with cavitation sufficient to cause a 3 percent loss of pump head |
RPM-GPM-FEET | N Qe0.5NPSH30.75 |
| S3/10 |
Approximate suction specific speed with cavitation sufficient to cause a 3 percent loss of pump head, for β1 = 100 |
RPM-GPM-FEET | |
| S40K |
Suction specific speed required to obtain 40,000 hour life, as defined by Vlaming |
RPM-GPM-FEET | N Qe0.5/NPSH40K0.75 |
| U1 |
Peripheral velocity of the inlet edge of the impeller vane, at the point where the vane joins the front shroud |
ft/sec | D1N/229 |
| W1 |
Velocity of liquid, relative to the impeller, just upstream of the impeller vanes |
ft/sec |
References
1. Stepanoff, A. J., Centrifugal and Axial Flow Pumps, John Wiley & Sons, Inc., 1948.
2. Grist, Edward, B.Sc., "Nett Positive Suction Head Requirements for Avoidance of Unacceptable Cavitation Erosion in Centrifugal Pumps," Paper No. C163174, 1974.
3. Vlaming, D. J., "Analysis of Cavitation Provides Advanced NPSH Estimates for Centrifugal Pumps," Oil & Gas Journal, November 19, 1984
4. Ross, Robert R., "Theoretical Prediction of NPSHR for Cavitation Free Operation of Centrifugal Pumps," United Centrifugal Pumps, about 1982.
5. Yedidiah, S., "Factor Pump Size into NPSH Comparisons," Power, June 1973.
6. Henshaw, Terry, "NPSHA-How Much is Enough?", Hydrocarbon Processing, Oct. 2004.
7. Deeprose, W.M. and McNulty, P.J., "Cavitation Noise in Pumps," Proc. 4th Conference of Fluid Machinery, Hungarian Academy of Sciences, Budapest, 1972.
8. Deeprose, W.M., King, N.W., McNulty, F.J., and Pearsall, I.A., "Cavitation Noise, Flow Noise and Erosion," National Engineering Laboratory, Department of Industry, East Kilbride, Glasgow, 1974.
9. Henshaw, Terry L., Advanced NPSH Workshop, PumpUsers EXPO 99, Nashville, TN, Sept. 1999.
10. Gongwer, Calvin A., "A Theory of Cavitating Flow in Centrifugal-Pump Impellers," ASME Hydraulic Div. Semi-Annual Meeting, Milwaukee, WI, June 1940.

