A significant factor in the design of a pumping system is the flow variation required by the process. Several pumps in parallel, variable speed pumps, pumps with on-off control and pumps with a control valve are some of the methods available for flow variation. A widely used method in the industry is to use control valves, generally located on the pump discharge in the pipe supplying process fluid. The flow could be used for different purposes—such as maintaining the level in a process vessel or in a boiler drum, or maintaining the flow in a pipeline or in the tubes of a fired heater. To understand how flow can be varied by a control valve, the system designer and operator need to understand the basic principles of how control valves behave.
The Control Valve
The flow rate through a control valve depends on the size of the valve, the pressure drop over the valve, the stem position and the flow properties. A simplified design equation for non-flashing liquids, ignoring the effects of the connected fittings, can be derived from References 1, 2 and 3 as Equation 1.
 Where: F = Fluid flow through the control valve Cv = Valve flow coefficient (at the full open) x = Valve stem position f(x) = Fraction of the valve size coefficient at any given valve stem opening indicating the inherent flow characteristics of the valve ∆Pv = Pressure drop across the control valve sp.gr. = Specific gravity of the fluid More detailed equations are available in the standards (References 1 and 2) and publications of the control valve manufacturers (Reference 4), also for flashing liquid services. The most common type valve characteristics are equal percentage, linear and quick opening type. Because of the distortion in valve characteristics in the extreme conditions of full open and full shut and because of the performance of the valve actuator and spring, the usable range is less than 0 percent to 100 percent.
Typically, this range is limited to about 10 percent to 90 percent of the valve opening. Distortion also occurs because of system losses that vary the pressure drop across the control valve in its operating range and result in valve characteristics that are different from the valve’s theoretical characteristics (Reference 6). The present analysis is based on a linear control valve, which is often the choice when constant control valve gain (the magnitude ratio of the change in flow through the valve to the change in valve travel under conditions of constant pressure drop) is required for accurate control of parameters, such as level or flow control. Processes require flow variations, either during plant capacity ramp up or ramp down. Flow variation is also required to handle fluctuations in the process parameters—such as drum level, thermal load variation requiring adjustment of cooling or heating fluid flow, or for adjusting pressure variation. To ensure controllability, the flow variation should not demand that the valve open either less than 10 percent or greater than 90 percent.
Where: F = Fluid flow through the control valve Cv = Valve flow coefficient (at the full open) x = Valve stem position f(x) = Fraction of the valve size coefficient at any given valve stem opening indicating the inherent flow characteristics of the valve ∆Pv = Pressure drop across the control valve sp.gr. = Specific gravity of the fluid More detailed equations are available in the standards (References 1 and 2) and publications of the control valve manufacturers (Reference 4), also for flashing liquid services. The most common type valve characteristics are equal percentage, linear and quick opening type. Because of the distortion in valve characteristics in the extreme conditions of full open and full shut and because of the performance of the valve actuator and spring, the usable range is less than 0 percent to 100 percent.
Typically, this range is limited to about 10 percent to 90 percent of the valve opening. Distortion also occurs because of system losses that vary the pressure drop across the control valve in its operating range and result in valve characteristics that are different from the valve’s theoretical characteristics (Reference 6). The present analysis is based on a linear control valve, which is often the choice when constant control valve gain (the magnitude ratio of the change in flow through the valve to the change in valve travel under conditions of constant pressure drop) is required for accurate control of parameters, such as level or flow control. Processes require flow variations, either during plant capacity ramp up or ramp down. Flow variation is also required to handle fluctuations in the process parameters—such as drum level, thermal load variation requiring adjustment of cooling or heating fluid flow, or for adjusting pressure variation. To ensure controllability, the flow variation should not demand that the valve open either less than 10 percent or greater than 90 percent.
System Head Curve
When specifying the pump and control valve, the designer must first develop the system head curve. The system head curve is the head required (m) to be developed by the pump at different flow rates in cubic meters per hour (m3/hr), ignoring the losses across the control valve. For systems comprised of static and dynamic losses such as the one shown in Figure 1, the system head curve can be represented as shown in Equation 2.
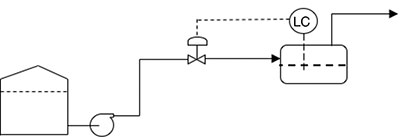 Figure 1. System with one control valve
Figure 1. System with one control valveHs = Hstatic + q x flow2 (Equation 2) Where: Hstatic = A constant, sum of the static head and pressure difference between source and destination q = A multiplying factor between the dynamic head and the square of the flow, which is a constant in turbulent flow condition Figure 2 shows a system head curve that was developed using: Hstatic = 50 m q = 0.009 [m head/ (m3/hr flow)]
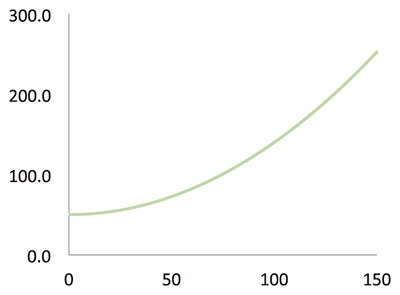 Figure 2. System head curve
Figure 2. System head curveFlow Variation
The next step is to define the range of flow at which the system is required to operate. The maximum and minimum flows should be defined at an early stage because they not only effect the selection of the control valve but also the minimum required head of the pump—this will become clear later in this article. Correctly defining the maximum flow intended from a control valve is important. Generally, a process is expected to operate at the design capacity, considered as 100 percent of flow condition. Any increase above 100 percent is expected to be temporary for purposes such as making up a drum level that has depleted because of some process upset. A margin should be provided above 100 percent of flow to recover the process parameters (drum level, in this case) to the normal value. These margins will depend on the nature of the disturbance. For level and flow control, they are generally about 10 to 15 percent. For restoring normal conditions in a distillation column, the margin for reflux control may be even higher at 20 percent. The maximum for the control valve will therefore be 110 to 120 percent of the design, depending on the nature of the corrective action. Most processes are expected to operate at 100 percent of design capacity for the best overall efficiency. However, they may have to be designed for operation at lower than 100 percent also. This lower flow capacity may occur for significant periods of time. Limitations of feed availability or product off take may force the operator to run the process at low loads. Generally, the turndown condition is defined during design so that all the components of the process are selected accordingly. The turndown condition in this case is to be treated as an alternate operating condition, from a control point of view. A margin below the turndown is required for the same reasons as the margin above the maximum flow. A temporary, high level in a boiler drum may have to be restored to normal by reducing the intake flow of the drum during turndown operation of the process. Therefore, the control valve’s minimum flow has to be computed considering about 10 to 20 percent below that needed for a steady state turndown condition of the plant, with the margin depending on the nature of the corrective action needed. The extreme maximum and minimum flows defined above with the margins should be matched to a control valve’s usable limits of 90 and 10 percent openings, respectively, to make best use the valve’s capabilities while also ensuring that the control valve is not forced to operate outside its recommended opening. Using the control valve from Equation 1 for the minimum and maximum flow rates, a relationship between the control valve (∆P) at minimum flow and the ∆P at maximum flow can be created. For valves with linear characteristics, the relationship is shown in Equation 3. ΔPminflow/ΔPmaxflow = [(0.90 x Fminflow) / (0.10 x Fmaxflow)] 2 (Equation 3)
System and Control Valve
A common practice in pump systems is to allow a minimum of 10 to 15 psi for the control valve’s pressure drop. Using Equation 3 and the control valve pressure drop at maximum flow, the designer can calculate the control valve pressure drop at minimum flow and at normal (100 percent) flow. The system head and the control valve head for minimum and maximum flow are shown in Figure 3. The straight lines are based on a case in which the maximum flow is 115 percent and the control valve head loss is 10 meters of water column (WC). Lines for different minimum flow cases (30 percent L, 35 percent L, 40 percent L, 45 percent L and 50 percent L) are also plotted.
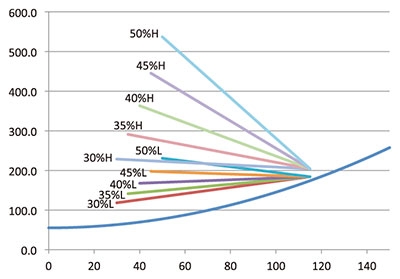 Figure 3. System head and control valve head for the conditions of minimum and maximum flow
Figure 3. System head and control valve head for the conditions of minimum and maximum flowIn a pump and control valve system, these lines should always fall on the characteristic curve of a centrifugal pump since the system head plus control valve loss has to equal the pump head. However, some of these lines can be seen to slope downward toward lower flow rates, which is unlike the shape of a centrifugal pump curve, which slopes down toward rising flow conditions. Depending on the shape of the pump curve, only one of these lines will best match the pump curve. In Figure 3, at 45 percent and higher minimum flow, the head requirement is seen to reduce with increased flow. In a second example, the above computations are based on a control valve with 30 meters of WC loss at maximum flow, instead of 10 meters of WC loss considered earlier. Loss at minimum flow is computed following the above steps. These lines (30 percent H, 35 percent H, 40 percent H, 45 percent H and 50 percent H) are also plotted in Figure 3. With these plots, even for the 30-percent turndown case, the head reduces with increased flow. The system head plus control valve head in this case will track the pump curve even to a lower value of minimum flow than was seen with the 10-meter WC head loss control valve.
Pump Characteristics
The impact of the flow turndown requirement on pump duty can be evaluated if the shape of the pump curve is known. A parabolic type pump characteristic curve developed using Equation 4 is considered for further study. Hpump = a + b x flow + c x flow2 (Equation 4) Where: a, b and c are constants For a typical pump, a family of pump curves will exist. The flow versus head relationship depends on the diameter of the impeller and can be calculated using the law of affinity shown in Equation 5. Hpump = (a + b x flow + c x flow2) x n2 (Equation 5) Where: n = the ratio of the impeller diameter, such as n = D2/D1 The curve with minimum n that meets the system plus control valve head, at minimum, normal and maximum flow conditions represents the optimum pump selection. These curves are plotted on Figure 4 showing 25.6 percent, 28.8 percent, 32.9 percent, 38.3 percent, 46.0 percent and 57.5 percent minimum flow cases with 115 percent as the maximum flow in all the cases. This is accomplished by simultaneous solution of the system head (Equation 2), control valve (Equation 3) and pump family of curves (Equation 5) to calculate a diameter ratio, n. The constants used for the pump curve were a = 200, b = -0.05 and c = -0.001.
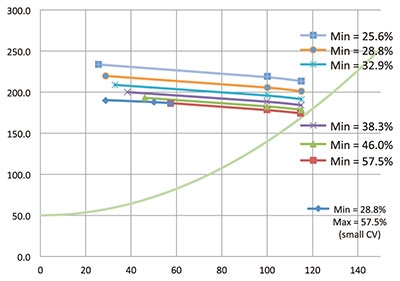 Figure 4. Family of pump curves
Figure 4. Family of pump curvesPump and Control Valve
As seen in Figure 4, about 45 meters less pump head is required at 100 percent of flow if the control valve minimum flow requirement is changed from 25.6 percent to 57.5 percent. Higher flow turndown results in higher control valve loss and, therefore, a higher pump head. This is also explained in Reference 3. The lower control valve loss at normal (100 percent) flow means continuously spending less energy since the system is expected to operate at 100 percent most of the time.
Deciding Flow Turndown
Extreme care should be taken when deciding the minimum flow required for control, and it is important not to aim for extremely low flow if it is unnecessary. If a very low flow condition is required on an infrequent basis, check to see if it can be handled in the field by using a small manual valve in the bypass of the control valve. Alternately, a smaller capacity control valve in the bypass of the main control valve can be provided, which will be sized specifically for the very low range of flow.
Split Range Control Valves
Figure 5 shows the two control valves, A and B, installed in parallel. Valve A is the original valve covering 57.5 percent to 115 percent of the flow range. Figure 4 shows (by simultaneous computation of Equations 2, 3 and 5) that a smaller control Valve B can be provided to cover 28.8 percent to 57.5 percent of the flow range with the same pump impeller diameter ratio, n, as was used for the 57.5 percent to 115 percent range larger control valve.
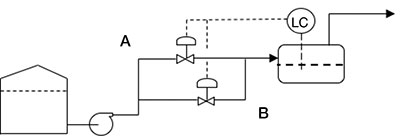 Figure 5. A system with two control valves
Figure 5. A system with two control valvesOverall, the two control valves can control through a range of 28.8 percent to 115 percent of the flow. Compared to having a single control valve to covers 28.8 percent to 115 percent of the flow, the two control valve arrangement consumes about 40 meters less pump head at 100 percent flow conditions. The energy saved by this alternate arrangement may justify the additional cost of the smaller control valve during the lifetime of the plant.
Selecting the Pump and Control Valve
The recommended steps for pump and control valve system design are summarized below:
- Prepare system head curves. In case the destination pressure is variable, prepare curves similar to Figure 2 for each destination pressure. Then prepare an overall system curve (see Figure 6) which should connect the extremes—such as maximum flow, maximum destination pressure on one side and minimum flow, minimum destination pressure on the other side.
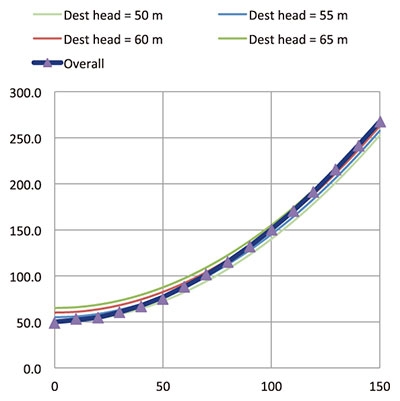 Figure 6. Overall system curve
Figure 6. Overall system curve- Specify the maximum and minimum flow requirements. Determine the flow required by the process through the control valve. Add positive and negative flow margins, respectively, depending on the control duty and determine the extreme maximum and minimum flows for which the valve should be selected.
- Fix about 10 to 15 psi (7 to 10 meters of WC) for the control valve loss at maximum flow. Using Equation 3, compute the control valve head required at minimum flow and at normal (100 percent) flow. Add the system head and control valve head requirement at minimum, normal and maximum flows and prepare plot similar to Figure 3.
- Based on Figure 3, specify the pump flow and head requirement at all three points. Pump vendors should also be asked to supply family of curves in the range of 110 percent to 90 percent of the head, which will help optimize the pump selection.
- Maximum flow—The pump is to provide no less than the specified head 10 to 15 psi (7 to 10 meters WC) at this flow condition (or the control valve will have to open more than the maximum recommended opening, which is not desirable).
- Normal (100 percent) flow—The pump should have the highest efficiency at this flow and head condition.
- Minimum flow—The excess above the minimum flow head should be as low as available from the pump (or the control will have to throttle below the minimum recommended opening, which is not desirable).
- The selected pump curve (see Figure 7) must touch all the three duty points. If this does not occur in the first operation, the two options using the vendor’s family of curves are:
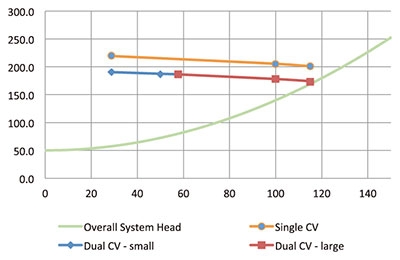 Figure 7. Pump curves
Figure 7. Pump curves- Increase the control valve’s minimum flow. Re-compute the required pressure drop at the minimum flow and at 100 percent of flow using Equation 3, and recreate Figure 3. Then superimpose a curve from the vendor’s family of curves. In this case, a second control valve in parallel will be needed for the low-flow-rate operation.
- Match the duty points with the vendor’s curve by increasing the control valve pressure drop (instead of 10 or 15 psi) at the maximum flow. This will avoid a second control valve but will have higher energy losses. Evaluate the two options and decide which provides optimum life cycle cost.
References
- ANSI/ISA-75.01.01 Standard, Flow Equations for Sizing Control Valves.
- ANSI/ISA–75.11.01 Standard, Inherent Flow Characteristic and Rangeability of Control Valves.
- A Rational Approach to CV sizing, Ind. Eng. Chem. Res., 1990, 29, 700-703. William L. Luyben.
- Emerson Control Valve Handbook.
- Pumping Systems Tip Sheet #10, March 2007. U.S. Department of Energy.
- Control Handbook, B. G. Liptak (chapter 36, “Applying Control Valves”).

