NPSH Calculation: A Step-by-Step Guide

This is the first article in a five-part series.

In the world of psychology and specifically in the area of introspective issues, it is often declared that, “what you resist will persist.”

You’ve heard it before, and here we go again. Allegedly, the most misunderstood concept in the pump world is net positive suction head (NPSH). I have written several articles on the subject and so have many other pump technicians or engineers and so-called experts.

The NPSH name itself, an acronym, confuses most pump neophytes. The subject and required calculations confounds people who are new to the industry, those on the periphery (operators or administrators) and professionals who incorrectly believe they fully understand the subject even after 25 years in the business.

I suggest we need to be concerned about this issue, because mistakes with respect to NPSH available (NPSHa) calculations are all too frequent and expensive to correct.

One of the fun parts of my position is teaching at several pump schools per year and devoting a major portion of the course to the subject of understanding the concept of NPSH and how to complete the calculations. In the teaching process, I cover the five main examples that you will likely encounter in normal industry applications. The examples are adapted from chapter 1 of the “Cameron Hydraulic Data Book.”

I will explain these five examples first in this column and over the next four months with the basic optimistic intent that once you learn these five examples and a few variations of each you will be able to handle the applications encountered in the real world. Between now and Thanksgiving, you may wish to read and file all five columns as a handy reference. As background, please re-examine two of my previous columns on the subject, one from Pumps & Systems August 2015 and the other from April 2018.

Definition of NPSH, NPSHa & NPSHr

The net positive suction head is the total suction head in feet of liquid (or meters), less the vapor pressure (in feet or meters) of the liquid being pumped.

Think of head as an energy level and not as a force-like pressure. All values are absolute.

NPSHa is measured at the pump centerline or the impeller eye. These two things can be at different places or elevations. Think of NPSHa as the liquid’s available energy level at the inlet of the pump or the eye of the impeller. The liquid will flash to vapor if there is not enough NPSHa. Do not confuse NPSHa with suction pressure. While suction pressure is in some ways a component in the mix, there is something more complex to the story.

NPSHa is the amount of NPSH that the system has available at the eye of the pump impeller. This NPSHa value is entirely a function of the liquid, its properties, ambient conditions and the suction system design and geometry. Essentially, the calculation is about the suction system itself and has nothing to do with the pump. This calculation should be completed by the system owner, the end user and/or their engineer or consultant. For liability reasons, manufacturers are normally directed to not be involved in the customers’ calculations; however, as time marches on, the manufacturer is getting more involved mostly as a preservation issue.

NPSH required (NPSHr) is most commonly determined by the pump manufacturer by empirical methods and using standards and specifications from the Hydraulic Institute (HI). NPSHr values are normally reported on the performance curves for the pump.

Note that NPSHr and NPSH3 are essentially the same thing. At the given operating point of head and flow, the pump is already slightly cavitating due to insufficient NPSH and the developed head has dropped by 3 percent while the flow rate is fixed at some value.

NPSH margin is how much the NPSHa value exceeds the NPSHr. There are guidelines for recommended or proper margins, and I say the higher the margin, the better. See ANSI/HI 9.6.1-2012 for more information on this subject.

NPSHa: Formula or the Figure?

I like to think of formulas as my “friends” because once I know the correct formula to use, I can simply fill in the values for the terms or components in the formula, complete the math steps and come up with the right answer. In college, we referred to this process as “plug and chug.” Some friends have told me that the moment I reference a formula in class or my articles, I lose 50 percent of my audience! So, for those of you that glaze over and hate formulas, perhaps you should study Image 1 for a few moments and see what’s going on there before we approach the formula.

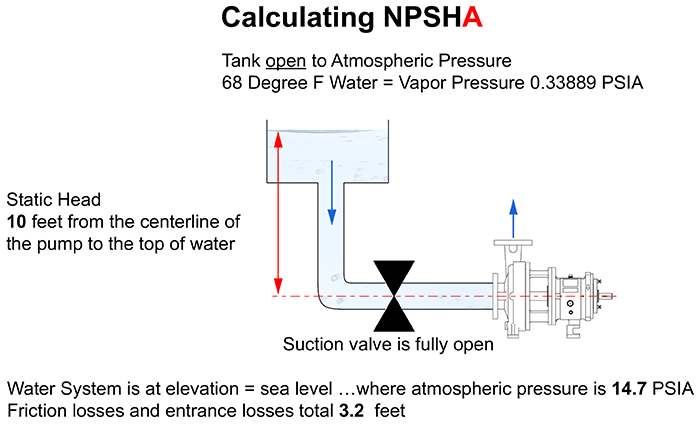
In Image 1, we have a tank of clear water at ambient temperature (68 F, which also means the specific gravity will be 1.0) and it is open to atmospheric pressure. Here, the tank and pump system are at an elevation near sea level. The top surface of the water level in the tank is 10 feet above the pump center line. We call this a “flooded suction” because the source of the liquid is above the pump impeller. There is adequately sized piping from the tank to the pump suction with an elbow and a fully open isolation valve. We will assume that the water level remains constant at 10 feet for the example, but in the real world you will want to calculate the NPSHa for the worse condition, which will likely be at a lower level.

At this point, with just the information I have given you from the figure, you have all the data you need to calculate the NPSHa, except the friction head. For this first example I will calculate the friction head to keep the problem simple. We will ignore velocity head since the value is normally small.

In future examples, we will discuss the methods of calculation for the friction head, and I will also calculate and show how the velocity head can affect the outcome or not.

To calculate NPSHa, you need to know:

• absolute pressure on or at the liquid surface
• static head, which is simply the vertical distance from the top of the water surface to the pump impeller eye (or pump centerline if they are the same)
• vapor pressure of the liquid being pumped, which you can easily calculate based on the temperature and is a value that is easy to look up
• friction head, which I have calculated and will advise for this example to be 3.2 feet
• velocity head, normally a negligible factor and for simplicity we will skip it this month and address in a later article in the series

Calculate the NPSHa for a Flooded Suction:

Back to the formula (yes I slipped it into the article).

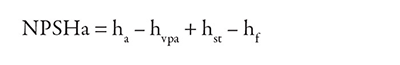
As mentioned before, you have the information to fill these four components in with real numbers and complete the calculation to determine NPSHa.

The first component in the equation (h_a) represents the value for the absolute pressure above the open water tank. It was given earlier that the system is at sea level.

The liquid in the open tank is subject to atmospheric pressure. At sea level, the atmospheric pressure can be assumed to be near 14.7 pounds per square inch absolute (psia), or 0 psi gauge (psig).

Note that variations in the atmospheric pressure can and will affect the NPSHa value.

Now you just need to convert the atmospheric pressure from psia to feet of head. Multiply 14.7 by 2.31, and the result is 33.957 feet, rounding to 34 feet. The value for the first component in the equation is 34 feet.

We will cover the effects of higher elevations and vacuum in later articles.

The second component in the equation is h_vpa, or the vapor pressure for the liquid at this given temperature of 68 F. To get the vapor pressure value, simply look it up in a reference book like the “Cameron Hydraulic Data Book.” The value (pressure of saturated vapor absolute) will typically be given in units of psia, will vary directly with the temperature and is also different for each liquid type.

The value you should obtain from your search is 0.33889 psia. Multiply that number by 2.31 to convert to head in units of feet. You will obtain the value of 0.7828 feet. We will round off to 0.783 feet. You now have the second value in the equation: 0.783 feet.

The third component in the equation is the static head (h_st). This is a vertical measurement from the surface of the liquid to the center line of the pump (impeller eye). Remember to figure for the worst case (lowest level expected). In our example, it was stated the static height is 10 feet. No need to convert as it is already in the correct units. You now have the value for the third component in the equation: 10 feet.

The fourth component (h_f) in the equation is the friction loss in the piping, which I previously supplied at a value of 3.2 feet. You now have all four values for figuring the answer.

Note that the given friction factor of 3.2 feet is a function of the liquid properties, the flow rate and the pipe (suction system) materials and geometry. You should understand in simple terms that for a given liquid flow rate, there will be friction losses for the pipe length, the elbow, the valve, the exit loss from the tank (large to small transition) and the entrance loss into the pump (change in diameters from the pipe to the pump nozzle). We will address some pipe friction fundamentals in the later examples in the coming months.

Lastly, remember we are not addressing the fifth factor in the formula, which is velocity head (h_vel). In a properly designed system (with Newtonian liquids in a nonslurry application), the value of velocity head will typically be under 1 foot in value.

The value for the velocity head component is positive.

For now, we have the four values required to fill in for the components and calculate the answer for NPSHa.

All units are in feet. The pressures are in absolute values.

Please work through the example to see if you get the same or similar value.

Next month, we will calculate NPSHa for a lift condition. Read it here.

In later editions, we will look at the effects of high elevations, hot liquids, hydrocarbons and pressurized suction tanks. We will also address suction conditions under vacuum.

References
Cameron Hydraulic Data Book, 16th edition

To read other articles in the 'Common Pumping Mistakes' column, go here.

1. For our metric friends, these components can also be in units of meters, but stay consistent with the units.
2. The components of vapor pressure and friction will always be a negative value and consequently always work against you.
3. Absolute pressure can be zero, but it cannot be negative (by definition).
4. Suppose the liquid source was below the pump instead of above? In the case of a “lift” where the liquid level is below the suction of the pump, (not a “flooded” situation) then that value for static height is negative (the situation is referred to as a “lift”) and this component in the equation now works against you.
5. We do not need to be concerned with the discharge side of the pump or system for NPSHa calculations.
6. In summary, most of the components in the NPSHa formula are working against you. You begin to understand why suction sources that are elevated, flooded, open to atmosphere and/or pressurized with the liquid at lower temperatures are desired.